Electronic magnitudes

Carriers and Fermi levels

Usually, the Fermi level, e_F, is calculated from the majority-carrier concentration. The process is explained in the Mechanisms section. But, also, the minority-carrier concentration can be found from Fermi level:

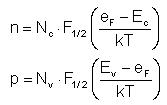
Where:

• N_c is the effective density of states in the conduction band.
• N_v is the effective density of states in the valence band.
• F_1/2 is the Fermi-Dirac function:

• See symbol list.

Intrinsic carrier concentration and intrinsic level

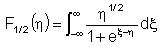
Intrinsic carrier concentration is defined as follows:

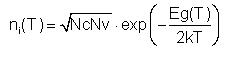
Where:

• N_c is the effective density of states in the conduction band.
• N_v is the effective density of states in the valence band.
• Eg is the band gap width.
• See symbol list.

Intrinsic electronic level is defined as follow:

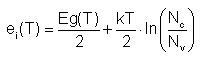
Where:

• Eg is the band gap width.
• N_c is the effective density of states in the conduction band.
• N_v is the effective density of states in the valence band.
• See symbol list.

Probabilities and charge states

DADOS implements two parameters depending on the charge:

• Diffusivities. Each species has its own migration energy and prefactor, that is assumed to be Fermi level independent.
• Proportion of concentrations. Probability of a particle "X" with charge "j" to be in a charge state. It can be calculated as follows:

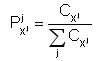
Where:

• C_Xj is the concentration of particle "X" with charge "j".

This probability is calculated using the expresions shown in the concentration ratio of charged species section.

Formation energies for charged species

The formation energy for a species "X" with charge "j" is given by:

Where:

• e_F is the Fermi level.
• e(j,j-1) is the electronic level for species X at temperature T. In the DDP file, this parameter is defined but for T = 0 K.

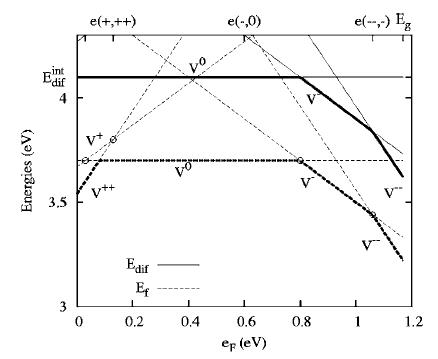
Formation energy for vacancies is plotted in dashed lines in the figure below. The total effective formation is the lowest one. That is given by:

Where:

• Ef is the formation energy.
• Em is the migration energy, assumed to be independent on the Fermi level.

Solid lines represent the activation energy of DC^* product of charged species.

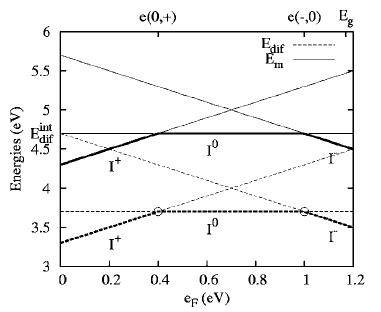
The situation for interstitials is analog.

Electric drift

The relation between the electric field (F) and the Fermi level (e_F) is:

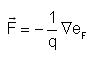
And, also, the relation between the formation energy (E_f) and the electric field (F) is:

The figure below shows electric drift as a natural consequence of the local dependance on the formation energies of charged particles.

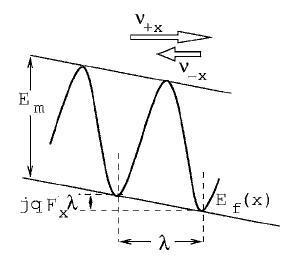
The relation between the migration frequency in the positive and negative directions along the x axis for a point defect with charge "jq" is (assuming constant band gap):

where:

• E_x is the electric field in "x" direction.
• λ is the capture distance.
• Ef is the formation energy.
• See symbol list.

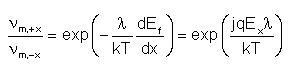
Sheet resistance

Let's suppose this structure:

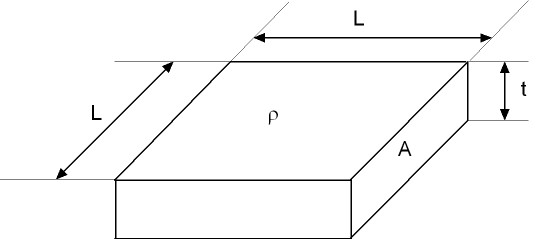
As its top surface is square, we can define the sheet resistance as follows:

Where

• r is the resistivity.
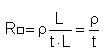
• L and t are the box dimensions (see figure).

In an electronic device, under extrinsic conditions, the sheet resistence can be approximated by:

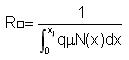
Where:

• x_j is the juction depth.
• m is the majority-carrier mobility.
• N(x) is the net impurity concentration.
• See symbol list.

For a given diffusion profile, sheet resistance is uniquely related to the surface concentration of the diffused layer and the background concentration of the wafer.