Charge model implementation

Simulated particles can have different charge states. As other parameters such as diffusion depend on the charge, DADOS implements charged particles as different species (click here for DADOS names):

DADOS assumes some hypotheses:

• Temperature dependance of charge levels and gap narrowing of charge levels dependance is the same as for the band gap.
• Charge is adapted and updated instantaneously, as charge reactions are much faster than structural ones.
• Substitutional dopants are always ionized and in the same charge state.

Band gap narrowing

Shifts of the minimum value of conduction band and maximum value of valence band are calculated by DADOS using the following expressions, according to Jain & Roulston model (Jain et al. 1991):

• For n-semiconductors:

• For p-semiconductors:

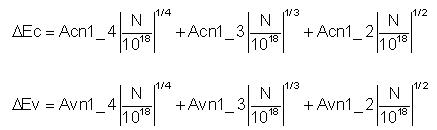
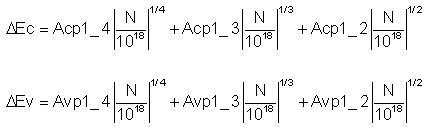
Where:

• N is the effective concentration of active dopants (with sign): N = N⁺ - N^-, where N⁺ is the active donors concentration and N^- is the active acceptors concentration.
• A??1_? are constants.

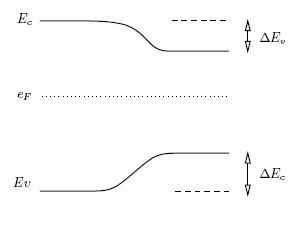
In every charge update, DE_c and DE_v are calculated.

For the rest of the electronic levels, DADOS assumes a proportional variation with the band gap narrowing as given by the expression:

Where:

• E_c is the conduction band energy.
• E_v is the valence band energy.
• e_? is a generic energy charge level.

See Sze 1981.

Charge attractions and repulsions

DADOS implements electrostatic interactions in both short and long range:

• For short range, repulsions are implemented by forbidding the interaction among charged particles (not neutral) with the same charge.
• For long range, electrostatic interactions (attractions and repulsions) are automatically included due to the electric drift in the migration (this process depends on the Fermi level).

Charge update

There are two mechanisms to control the charge states probabilities:

• Dynamic update: The charge state is updated whenever the particle jumps, in order to follow the probabilities of charged species in each box. These probabilities have been previously calculated as a function of the Fermi level during the static update. This is suitable for particles jumping at low frequencies.
• Static update: The charge state is updated every some time.

DADOS uses a counter to simulate charge update and calculate Fermi level in all boxes. Every time an electrically active dopant is created or destroyed, the counter is raised. When the counter value is higher than a threshold, DADOS updates the charge state for all particles.

The threshold changes during the simulation, according the charge variations. With ChargeVarPercent, this mechanism can be controlled. This parameter indicates the maximum relative error allowed in Fermi level updates. The higher ChargeVarPercent is, the less updates are done. It is NOT recommended changing this parameter because DADOS is very sensitive to variations in this value. Modifications of this parameter should be allowed only for advanced users because:

• If ChargeVarPercent is very low, calculations will be made very frequently, and the simulation will become slower.

• If ChargeVarPercent is very high, updates will not be frequent enough, and physically incorrect values might be obtained.

Electric drift implementation

As the formation energy of charged species depends on the Fermi level, mobile charged point defects are going to find an energy barrier to jump into boxes in which the formation energy is higher. Electric drift is implemented in DADOS as a discrete process, setting a constant Fermi level for each box:

Fermi level calculation

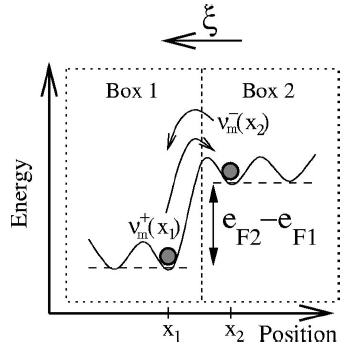
DADOS calculates the Fermi level in each box using its smoothed dopant concentration, N_sm:

• If N_sm > 0 (n-type boxes):

• If N_sm < 0 (p-type boxes):

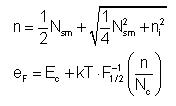
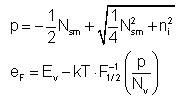
Where:

• E_c is the conduction band energy.
• E_v is the valence band energy.
• F_1/2 is the Fermi-Dirac function and F^-1_1/2 is its inverse. Those functions, when required, are calculated with analytical approximations.
• n_i is the intrinsic carrier concentration.
• See symbol list.

See Sze 1981.

Smoothing the dopant distribution

DADOS checks all the boxes and stores the dopants per box. After that, DADOS smoothes the dopant concentration using a locally-dependent radius equal to the Debye length:

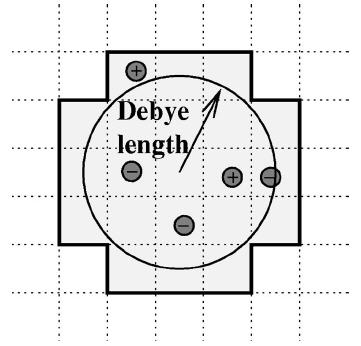
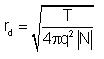
Where:

• N is the effective concentration of active dopants (with sign): N = N⁺ - N^-, where N⁺ is the active donors concentration and N^- is the active acceptors concentration.
• See symbol list.

In order to avoid excessive computerization, the maximum number of boxes for Debye length is set to 7.

The smooth dopant concentration, N_sm, will be used in the Fermi level calculation of each box using the neutrality approximation. This smoothed neutrality approximation is a computer-efficient method with intermediate precision between the simple local neutrality approximation and the time consuming solution of Poisson equation.

Temperature dependance of band structure

Band gap width

The band gap width depends on the temperature, T, following the expression:

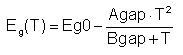
Where:

• Eg0 is the band gap width at 0 K.
• Agap and Bgap are constant parameters.
• See symbol list.

Charge levels

We denote by e_? the charge level associated to a charged particle, ?, at the current temperature, T. e_? is measured from the valence band edge.

DADOS assumes that all charge levels temperature dependancy is the same as band gap width one, thus:

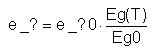
Where:

• e_?0 is the charge level at 0 K.
• Eg(T) is the band gap width at temperature T.

Related physical magnitudes

• Equilibrium concentration of charged species.
• Formation energies of charged species.

Effective density of states

DADOS implements the states density in both conduction and valence band as follows:

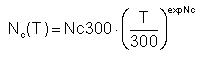
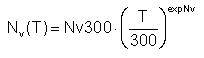
Where:

• Nc300 and Nv300 are the effective densities of states in the conduction and valence band respectively at 300 K.
• expNc and expNv are exponents to calculate the density of states in the conduction and valence band respectively.
• See symbol list.