Diffusivities

Direct diffusivity of single impurities

For single impurities non assisted by interstitials or vacancies (e.g. F, H,...):

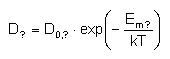
Where:

• D_0,? is the prefactor of diffusivity for particle "?".
• E_m? is the migration energy for particle "?", Em_?.
• See symbol list.

Effective diffusivity of native defects

For I or V, the relevant magnitude is the DC product. Thus, the effective diffusivity of I or V can be defined as (Fahey et al. 1989):

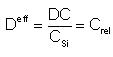
Where:

• D is the prefactor of diffusivity.
• C^* is the concentration under equilibrium conditions.
• C_Si is the atomic density in crystalline silicon.

Thus:

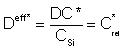
The activation energy of D^eff* is:

Edif = Ef + Em

Where:

• Ef is the formation energy.
• Em is the migration energy.

Silicon self-diffusion

The diffusivity of silicon in silicon (self-diffusion) is given by (Bratch et al. 1998):

Where f_x is taken to be 0.72 for interstitials and 0.5 for vacancies.

Effective diffusivity of dopants

For immobile impurities, diffusivity through mobile pairs, AX:

Let's use the boron (negative ion is substitutional positions).

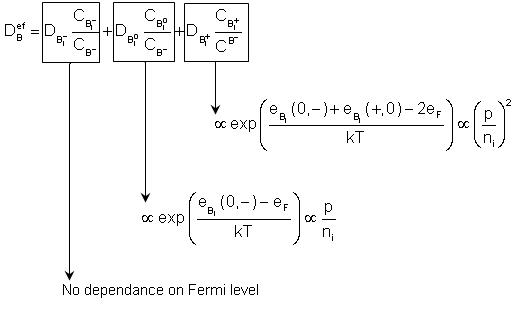
Where:

• D^ef is the effective diffusivity.
• C_X is the concentration of X.
• e_X is the energy level or X.
• e_F is the Fermi level.
• p is the holes concentration.
• n_i is the holes or electrons intrinsic concentration.
• See symbol list.

The proportionalities to p/n_i and (p/n_i)² are valid only within the Maxwell-Boltmann approximation (non-degenerated material).

The activation energies of the terms in the previous equation (diffusion energies, E_dif) are represented in the figure below. The diffusion energy value for boron under intrinsic conditions in the figure below (E_dif^int) will be similar to the activation energy of the Arrhenius plot of equilibrium boron diffusivity in intrinsic condition. In the figure, it can be seen that B_i⁰ is a metastable state but is the main contributor for boron diffusion in a wide range of Fermi levels. All the three terms of the equation are proportional to:

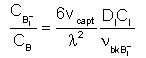
Note that D^IC^I is the DC product of neutral interstitials. Thus, boron diffusion does not depend on the charge states of I, but on those of B_i.

See Fahey et al. 1989 and Martin-Bragado et al. 2005.

Long-hop distance

In the figure below, we can see that, after Bi formation, this point defect migrates through the material an average distance, Λ (long-hop distance) until it breaks up.

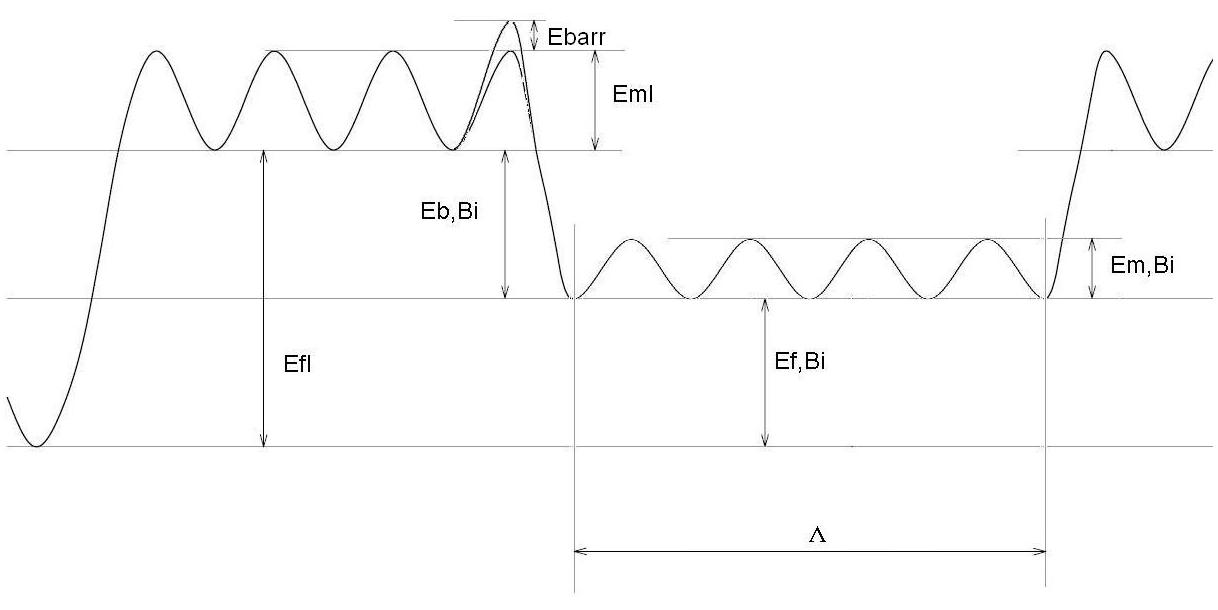
The long-hop distance can be expressed as:

The energy associated to this process can be calculated as follows:

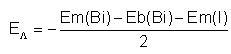
This energy is negative.