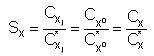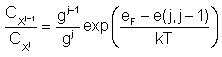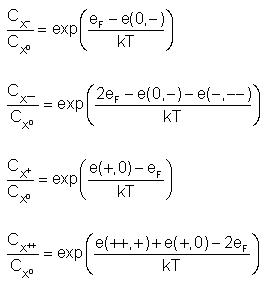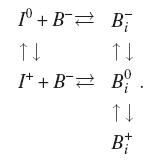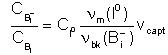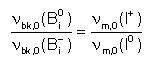Concentrations

Equilibrium concentration of neutral native defects

The concentration of single neutral native defects under equilibrium conditions is determined by:

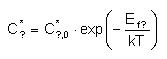
Where:

• C_?,0^* is the prefactor, related to DADOS parameter C0relEq_? under equilibrium conditions as follows:

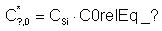
• E_f? is the formation energy, that is equal to the input parameter Eform_?.
• See symbol list.

Supersaturation

Supersaturation is defined for both interstitials and vacancies as the ration between its concentration and the equilibrium one.

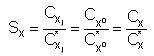
Supersaturation does not depend on the charge state. This is because the rations C^j-1/C^j do not depend on the excess of defects, but only on Fermi level (Fahey et al. 1989).

Concentration ratio of charged species

The relative concentration between the of charged species is:

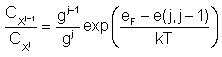
Where:

• C_Xj is the concentration of X with charge "j".
• g^j is the degeneracy factor. We assume it to be the same for all charge states, i.e. there is no entropy change associated to charge transitions.
• e_F is the Fermi level.
• e(j,j-1) is the electronic level for species X at temperature T. In the DDP file, this parameter is defined but for T = 0 K.
• See symbol list.

According to the equation, the following expressions are valid:

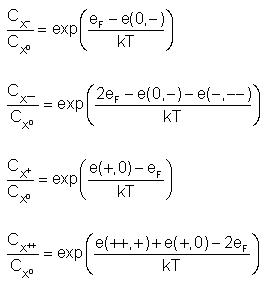
See Fahey et al. 1989 and Martin-Bragado et al. 2005.

Break-up of charged pairs: Boron case

The pairing, break-up and charge reactions related to B_i are represented by the reactions:

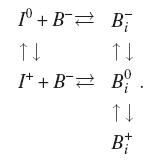
Comments

• Substitutional boron is always immobile and ionized (B^-).
• Horizontal reactions (pairing and break-up) conserve the charge while vertical reactions establish the electrical equilibrium.
• The rate of the horizontal reactions will not depend on Fermi level.
• Direct break-up of B_i⁺ is not included because I⁺⁺ is not implemented.
• The activation energy for B_i^- break-up will be Eb(B_i^-)+Em(I⁰) (see figure below), where Eb is the binding energy and Em is the migration energy.

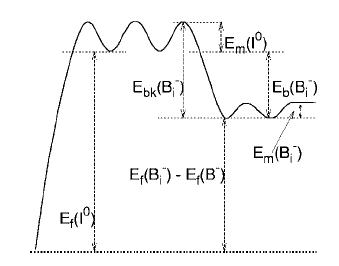
• Considering energy conservation, we can conclude: Eb(B_i⁰)=Eb(B_i^-)+e_Bi(0,-)-e_I(+,0),where e(j,j-1) is the electronic level for species at temperature T. Electronic levels scale with gap energy, introducing a slight temperature dependance in binding energy for B_i⁰.
• The number of broken B_i^- per unit of volume and time will be C_Bi-n_bk(B_i^-) and the number of new formed C_B-C_I0ν_m(I⁰)v_capt, where v_capt is the effective capture volume for pairing reaction. Consequently, in local equilibrium conditions:

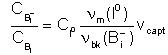
• And, from equilibrium conditions it can be also derived that the break-up prefactors, ν_bk,0 must fulfill:

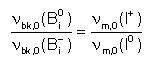
See Martin-Bragado et al. 2005.
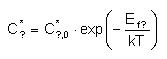