
|

|
| A mis padres |
| y a Susana |
Asímismo, quisiera dar las gracias al Director del Departamento de Electrónica, el Dr. D. Juán Barbolla Sancho por la oportunidad de trabajar en este grupo de investigación.
Mi agradecimiento al Dr. D. Martín Jaraiz Maldonado y al Dr. D. Ángel Rubio Secades por las discusiones en las que intentamos hacer que esto fucionara.
Quiero extender mi gratitud a todos los miembros del Departamento: a D. José Emiliano Rubio, por ser tan buen compa~nero de viaje, a D. Salvador Due~nas, Da Elena Castán, Da Lourdes Enriquez, Da Lourdes Pelaz, D. Luis Marqués, D. José Vicente, D. Pedro Castrillo, D. Luis Quintanilla, Da Rosa Pelaez, D. Angel Vegas, por estar ahí en todo momento, y a Da Ruth Pinacho además por su hospitalidad.
No quisiera olvidarme de mis compa~neros y amigos desde el comienzo de la carrera, D. Oscar Alejos y D. Ismael Barba. Sólo ellos han soportado estoicamente mi compa~nía todos estos a~nos.
Por último, quisiera agradecer a todo el mundo que de una forma u otra ha estado implicado en el desarrollo de este trabajo, su paciencia y apoyo.
Gracias a todos y a los demás también.
Uno de los procesos de la Tecnología Microelectrónica (fabricación de Circuitos Integrados) cuya finalidad principal es la impurificación precisa del material, es la implantación iónica, sin que esta sea su única utilidad.
La implantación iónica consiste en la proyección contra el material (blanco) de un haz de iones (proyectiles) acelerados con suficiente energía para penetrar más allá de las capas superficiales. El sistema que realiza esta operación es el implantador iónico. Es obvio, dadas las dimensiones actuales de los dispositivos y otros elementos electrónicos que forman los circuitos integrados, que el control de la distribución de los iones que han penetrado en el material (perfiles de implantación) es imprescindible. Cómo conocer estos perfiles es uno de los temas de máximo interés en nuestros dias. Como en tantos otros casos, puede accederse al resultado a través del análisis experimental de los perfiles de implantación (caracterización) o mediante modelos matemáticos de naturaleza predictiva que, actualmente, pasan forzosamente por el ordenador (simulación).
Las metodologías usadas en el cálculo de perfiles por ordenador son varias: Principalmente Dinámica Molecular y Aproximación de Colisiones Binarias. La primera es de gran exactitud, pero imposible de aplicar a sistemas con un gran número de partículas y con las energías de implantación actuales por el tiempo de cálculo requerido. La Aproximación de Colisiones Binarias (BCA) no es tan exacta, pero la modelización de la trayectoria del ion en el material mediante sucesivas colisiones del mismo con un número muy reducido de átomos del blanco no es tan costosa en tiempo de cálculo y sus resultados son adecuadamente útiles a tecnólogos y dise~nadores.
A este tipo de simulación, a su entendimiento y su mejora, hemos dedicado nuestro trabajo. Nuestras aportaciones han sido básicamente en los siguientes temas, que también han servido para marcar nuestros objetivos, a la vez que para estructurar esta memoria:
Por un lado hemos realizado un estudio sistemático de la situación actual de la simulación de la implantación iónica. Nuestra motivación y la valoración de su estado ha sido incluida en el Capítulo 1.
En el Capítulo 2 desgranamos las ideas básicas acerca de lo que es el proceso de la implantación iónica, cual es la problemática que lo rodea y cuales son algunas de las técnicas de medida empleadas para conocer lo que realmente se obtiene. Tambien estudiaremos algunas de las aplicaciones típicas de este proceso tecnológico.
Dado que nuestro problema es simular la implantación iónica repasaremos, en el Capítulo 3, las técnicas de simulación empleadas hasta la fecha, así como otros algoritmos que mejoran el ruido estadístico en alguna de estas técnicas.
En cuarto lugar hemos considerado el aspecto computacional del problema. Se ha desarrollado un nuevo programa escrito en C++ en el que se ha tratado de optimizar su estructura y operación en relación con el problema concreto a simular, que ha sido el acanalamiento de los iones en el material y la influencia que sobre él tienen tanto la estructura del sólido (distribuciones de carga, modelos de potenciales de interacción) como las características del proyectil. Una de las aportaciones más interesantes ha sido la introducción de un algoritmo de mejora estadística de los resultados. Con ello se han conseguido simular perfiles de implantación con un muy reducido tiempo de cálculo. El Capítulo 4, contempla, pues, el funcionamiento y la optimización del programa de cálculo.
Con nuestro programa adecuadamente operativo hemos contemplado los diversos aspectos físicos de la interacción del ion con los átomos del material y que son
a) Las interacciones nucleares, tanto binarias como simultáneas, que vendrán afectadas por el potencial interatómico.
b) Frenado inelástico al interaccionar proyectil y blanco con las cargas electrónicas respectivas.
Esto constituye el núcleo del Capítulo 5 en el que describiremos los modelos más adecuados para la implantación en general.
Y finalmente, en el Capítulo 6 analizaremos la aplicación de nuestro programa a la implantación en silicio, estableciendo su valor predictivo en comparación con resultados experimentales y sus límites de aplicabilidad para los diferentes iones y sus diferentes energías.
El autor
 Si {{ 100}} con 0.5
keV.
Si {{ 100}} con 0.5
keV. Si {{ 100}} con 2 keV.
Si {{ 100}} con 2 keV. Si {{ 100}} con 15 keV.
Si {{ 100}} con 15 keV. Si
{{ 100}} con 35 keV.
Si
{{ 100}} con 35 keV. Si {{ 100}} con 80
keV.
Si {{ 100}} con 80
keV. Si {{ 100}} con 140 keV.
Si {{ 100}} con 140 keV. Si {{ 100}} con 700 keV.
Si {{ 100}} con 700 keV. Si {{ 100}} con 2 keV.
Si {{ 100}} con 2 keV. Si {{ 100}}
con 15 keV.
Si {{ 100}}
con 15 keV. Si {{ 100}} con 35
keV.
Si {{ 100}} con 35
keV. Si {{ 100}} con 80 keV.
Si {{ 100}} con 80 keV. Si {{ 100}} con 280 keV.
Si {{ 100}} con 280 keV. Si {{ 100}} con 500 keV.
Si {{ 100}} con 500 keV. Si {{ 100}} con 2400 keV.
Si {{ 100}} con 2400 keV. Si {{
110}} con 15 keV.
Si {{
110}} con 15 keV. Si {{ 110}} con 35
keV.
Si {{ 110}} con 35
keV. Si {{ 110}} con 80 keV.
Si {{ 110}} con 80 keV. Si {{
100}} con 180 keV.
Si {{
100}} con 180 keV. Si {{ 100}}
con 15 keV.
Si {{ 100}}
con 15 keV. Si {{ 100}} con 100
keV.
Si {{ 100}} con 100
keV. Si {{ 110}} con 50 keV.
Si {{ 110}} con 50 keV. Si {{ 110}} con 100 keV.
Si {{ 110}} con 100 keV.| En esta vida caduca |
| el que no trabaja no manduca |
| ~ Refrán ~ |
El desarrollo de la tecnología microelectrónica a lo largo de los últimos 30 a~nos ha sido posible gracias al esfuerzo realizado en la investigación básica de los procesos tecnológicos que forman parte de ella. Sin embargo, esta investigación básica tiene un coste muy elevado dado que requiere de sistemas de investigación muy especializados. En un intento, de abaratar costes y de entender qué ocurre dentro del semiconductor, se ha desarrollado a lo largo de estos a~nos, la simulación de los procesos tecnológicos y de los efectos físicos que conllevan.
Cuando se desarrolla un simulador, se intenta solucionar un problema dado, para poder dise~nar y fabricar dispositivos más rápidos, más peque~nos y con menos problemas. Por ello, las soluciones que se aportan pueden carecer de un sentido físico estricto del problema planteado, empleandose un modelo fenomenológico que tenga un conjunto de parámetros ajustables, que permita obtener las soluciones para cada tipo de problema.
Esta aproximación está justificada desde el punto de vista de la industria, dado que esta progresa gracias a la fabricación y venta de los dispositivos y circuitos dise~nados. Si bien es cierto, que el espiritu de los que investigan y modelan estos simuladores está orientado a conseguir explicar sin fisuras el comportamiento físico que quieren simular.
En el International Technology Roadmap for Semiconductors (ITRS) de la Semiconductor Industry Association en las ediciones de 1997 y 1999 se comenta que para alcanzar las metas establecidas en el mundo de los semiconductores en los próximos a~nos es preciso investigar a fondo lo que ocurre llegando a nivel atómico y es necesario desarrollar herramientas manteniendo un compromiso entre velocidad y precisión:
Continuum physics models are no longer sufficient below 100 nm. Tools are needed for the physical and chemical processes at an atomic level. These tools will require much more computational resources as well as advaced skills in basic sciences. A hierarchy of tools is needed that is self-consistent and allows the tradeoff of speed versus accuracy.
| ITRS 1997 |
.. Precise modeling of the various phenomena observed in processes at the electron level must be established. In contrast to conventional models, wich assume the physical continuity of materials, alternative solutions at nodes bellow 100 nm may include the adoption of discrete modeling procedures: for example, the Monte Carlo methods, in wich atoms and electrons are treated as particles, or the quantum dynamic calculation methods, wich are based on solving Schroedinger’s equation.
.. Atomistic process modeling will be needed at the far end of the Roadmap. Regardless of the particular technology direction, it is assumed that the ability to manipulate and control materials to atomic layer tolerances will be required.
| ITRS 1999 |
La motivación, por tanto, que nos ha llevado a la investigación y desarrollo de un simulador del proceso tecnológico microelectrónico denominado implantación iónica, es conseguir un modelo físico atomístico con el menor número de parámetros ajustables que sea capaz de reproducir y predecir el comportamiento del proceso bajo diferentes condiciones, sin olvidar que nuestro simulador debe responder con la solución del problema en un tiempo razonablemente corto.
Existen varias formas de abordar la modelización de la implantación iónica como veremos más adelante. Sin embargo, una descripción muy detallada de lo que ocurre teniendo en cuenta todos los detalles es computacionalmente muy costosa y en algunos casos simplemente es inabordable. Hemos intentado llegar a un compromiso entre la velocidad de resolución y la exactitud de los resultados obtenidos, manteniendo siempre el compromiso de llegar a un modelo físico razonable y con el menor número de parámetros ajustables.
Actualmente, en el ámbito de la microelectrónica existen varios simuladores del proceso tecnológico que nos ocupa, que dan con bastante precisión la solución a los problemas planteados, sin embargo, y como hemos comentado anteriormente, emplean un conjunto muy amplio de parámetros para hacer encajar los resultados simulados con los resultados experimentales. A modo de ejemplo, un fragmento literal de uno de los artículos de la bibliografía [81] publicado este mismo a~no hablando de su simulador CRYSTAL-TRIM en el punto de conclusiones:
A minimum number of empirical parameters is used: Depending on the ion species two to four parameters are required to apply the semi - phenomenological model for the electronic energy loss. Their values are obtained from depth profiles of low dose implantations at different directions of incidence. For each ion type two parameters are necessary to employ the phenomenological model for the enhanced dechanneling due to ion-beam-induced damage. Their values are determined from experimental data on the dose dependence of the shape of depth distributions. A third set of two to five parameters has to be used to describe accurately the implantation profiles in amorphous and amorphized Si. It should be noted that the different parameters set mentioned are completely independent from each other.
Parece claro, pues, que en los simuladores actuales se ajustan los modelos para poder seguir adelante en el desarrollo de dispositivos, pero sin dar una visión física de la solución.
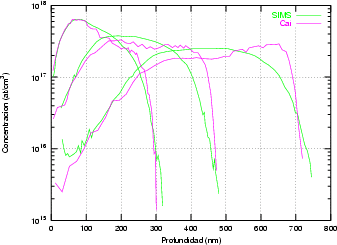 a) Boro (0,0) implantado en silicio {100} con 15, 35 y 80 keV. 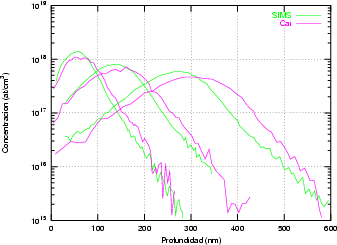 b) Boro (7,30) implantado en silicio {100} con 15, 35 y 80 keV. 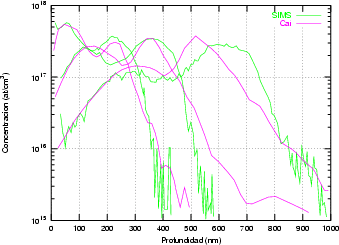 c) Boro (0,0) implantado en silicio {110} con 15, 35 y 80 keV.
|
Otros autores [45] utilizan las constantes físicas del material, (temperatura de Debye), como parámetros para ajustar sus simuladores dependiendo de las condiciones de implantación, para que estos reproduzcan los resultados experimentales. Estos simuladores no pueden pretender ser predictivos. Puesto que predicen a posteriori los perfiles experimentales.
En algunos simuladores, como UT-MARLOWE [72, 55, 56, 54, 115, 114], se emplea un modelo de frenado electrónico diferente dependiendo del proyectil implantado, teniendo cada modelo su conjunto de parámetros ajustables. No obstante, hubo un intento de uniformizar modelos en este programa [19]. En la figura 1.1 pueden verse los resultados obtenidos para diferentes energías y canales al implantar boro. Los resultados son mucho peores que los obtenidos por el mismo programa utilizando su conjunto de modelos fenomenológicos con parametrizaciones a medida. La conclusión de este artículo [19] es que el modelo de colisiones binarias no es capaz de dar mejores resultados, y que es necesario ir más al detalle empleando una modelización de dinámica molecular [8], que es un modelo de cálculo dos órdenes de magnitud más lento.
Es posible obtener soluciones mejores de forma rápida, empleando el modelo de colisiones binarias, sin emplear una bateria de parámetros ajustables. En este trabajo describimos nuestros modelos y los resultados predictivos que proporciona.
El International Technology Roadmap for Semiconductors (ITRS) de la Semiconductor Industry Association (SIA) es la referencia obligada para conocer qué es lo que la industria de semiconductores requiere, tanto en investigación como en desarrollo, para seguir reduciendo las dimensiones de los dispositivos al tiempo que se aumenta la frecuencia de funcionamiento de los mismos. Es decir, para que el negocio de los semiconductores siga creciendo.
En su edición de 1997 se marcaba como punto clave para la modelización y simulación el desarrollo de modelos para la simulación de la implantación iónica. Dada la potencia computacional de los ordenadores de entonces, se marcaba como fecha de introducción en la cadena de producción de este tipo de herramientas basadas en simulaciones Monte Carlo (BCA) el a~no 2001. A partir de entonces, sería abordable el problema con Dinámica Molecular, que proporciona una modelización más exacta, pero que era computacionalmente inabordable en los casos prácticos.
No solo se esperaba el aumento de la velocidad de los computadores para hacer factible la resolución de estos problemas, sino que se incentivaba el estudio de técnicas de reducción de la varianza para minimizar el ruido en tiempos de simulación aceptables1.
En su edición de 1999 el ITRS en su apartado de modelización y simulación, incide en conseguir mejorar la eficiencia en el desarrollo y producción, para lo que son necesarios modelos teóricos que cubran todas las posibilidades, así como mejoras en la velocidad y precisión de los mismos.
Puntos interesantes de la implantación iónica son la modelización de implantaciones a muy baja energía para hacer uniones muy estrechas (ultra-shallow junctions), el da~nado en la implantación, la amorfización del material y la obtención de perfiles 2D. También es interesante la implantación a alta energía para el aislamiento de dispositivos en pozos (wells).
Vistas las necesidades y antes de decidirnos a abordar el problema de realizar un simulador desde cero, analizamos las diferentes soluciones existentes, así como sus pros y y sus contras.
Proceso de Medida: técnica SIMS
Unido a todo esto, está la disparidad entre las diferentes referencias bibliográficas en las que se pueden encontrar disparidades en el rango de los perfiles de hasta un 50 % para las mismas condiciones de implantación7.
Nuestra valoración pués de los perfiles experimentales, es que no son una reproducción exacta de lo que ocurre en la realidad, sino que tienen, como todas las medidas experimentales su error asociado. Por tanto, cuando comparemos el resultado de nuestras simulaciones con los resultados medidos experimentalmente con la técnica SIMS habrá que tener en cuenta que el error experimental puede ser notable.
Los podemos clasificar en tres grupos dependiendo de la técnica de simulación empleada8. En la tabla 1.2 encontramos un resumen.
Nuestras conclusiones, después del estudio de los diferentes tipos de herramientas a través de su uso (TRIM, MARLOWE) o de la literatura y de las necesidades del ITRS, son:
Por consiguiente nuestros objetivos serán: obtener un programa de simulación moderno, que incluya todas la innovaciones aparecidas hasta el momento, y otras mejoras como un modelo de frenado más general que no incluya un gran conjunto de parámetros ajustables para cada material, que permita la predictibilidad; optimizar la velocidad de funcionamiento con paralelismo y técnicas de reducción de la varianza novedosas.
Nuestra elección será la técnica de simulación BCA.
En este trabajo no se pretende simular la implantación iónica teniendo en cuenta la recombinación y da~nado presentes durante el proceso, que serán tema continuación de este trabajo. Tampoco pretende tener en cuenta procesos posteriores como el recocido y difusión de las impurezas. Se tendrán en cuenta los aspectos físicos del problema y los parámetros tecnológicos del mismo. En resumen, queremos realizar un simulador que sea capaz de predecir los perfiles de impurezas implantadas con diferentes energías, iones, orientaciones cristalográficas, y composición del material blanco (óxido).
| La más larga caminata |
| comienza con un paso |
| ~ Provervio hindú ~ |
La implantación iónica consiste en el bombardeo de un material con átomos ionizados con suficiente energía, para penetrar más allá de las capas superficiales [98]. El objetivo de tal implantación es, principalmente, la impurificación del material.
La idea de la impurificación de semiconductores por bombardeo iónico fue patentada por William Shockley [92] en 1954 en los laboratorios Bell. Más tarde, en la década de los 60 fue desarrollado el método de la implantación iónica que, en los últimos 30 a~nos se ha convertido en una de las formas más habituales de introducir impurezas en los semiconductores.
La profundidad alcanzada por los iones es aproximadamente proporcional a su energía inicial y es interesante poder controlarla. Esta técnica permite la impurificación de los materiales semiconductores con casi cualquier elemento, independientemente de su solubilidad en el material1.
Las ventajas del empleo de la implantación iónica con respecto a otras técnicas son las siguientes:
No obstante, también tiene desventajas que limitan sus posibilidades de aplicación:
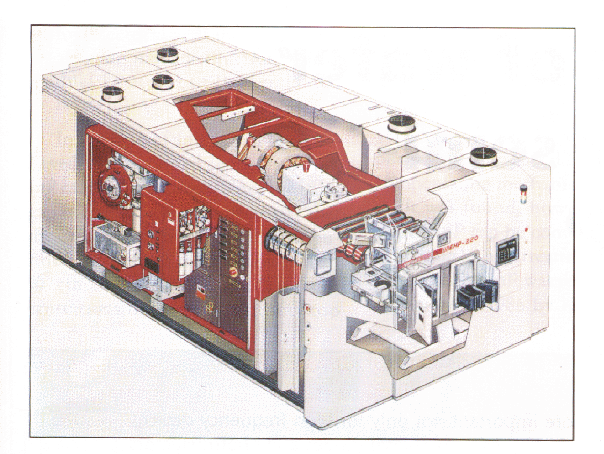
Para poder comprender en detalle, en qué consiste el proceso tecnológico de la implantación iónica, mostraremos primero, en la sección 2.2, la estructura de un implantador iónico comercial que nos dará una versión real del problema a tratar.
En la sección 2.3 estudiaremos las técnicas de medida más comúnmente empleadas para conocer qué es lo que realmente tenemos después del proceso. Y por último, en la sección 2.4 veremos algunas de las aplicaciones que hacen interesante el estudio y uso de la misma, sobretodo en microelectrónica.
En la figura 2.1 se muestra un implantador iónico comercial [24, 98]. Estos aceleradores de partículas se adaptan a la aplicación concreta para la que se dise~nan, tanto en rangos de energía que pueden proporcionar, como en fuentes de iones de que disponen. Básicamente están compuestos de:
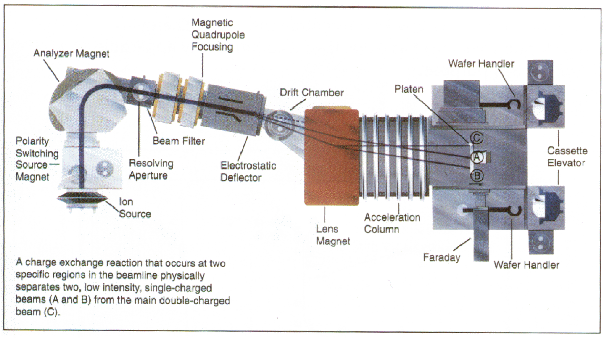
|
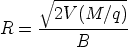 | (2.1) |
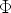 , implantada (Fig. 2.2):
, implantada (Fig. 2.2):

Las colisiones ion - blanco pueden producir electrones de baja energía que escapan de la oblea falseando la medida de la dosis. Para evitarlo se encierra la oblea en una caja de Faraday polarizada con una tensión alta con respecto a la oblea para obligar a los electrones a regresar a la misma.
Puede producirse un sputtering de los elementos que componen el implantador, como las ranuras de apertura, quedando implantadas impurezas (átomos pesados) no deseadas. Para minimizar el efecto se fabrican las rejillas de apertura de carbono o silicio que no serán eléctricamente activos.
Exiten por tanto una multitud de efectos parásitos que afectan a la precisión de las implantaciones.
Existen muchas técnicas diferentes para la medida de perfiles de impurezas. Nos centraremos en algunas de las más utilizadas en el campo de la tecnología electrónica6.
La técnica SIMS7 consiste en el bombardeo de la superficie de la muestra con un haz de iones primarios de baja energía seguido de una espectroscopía de masas de los iones secundarios emitidos [9]. Es una técnica que destruye la muestra medida.
El primer sistema de microanálisis SIMS fue construído en la decada de los 60 bajo un contrato de la NASA para analizar la composición de las rocas lunares. Encontraron que funcionaba mejor de lo que esperaban y empezó entonces su comercialización para la industria de materiales electrónicos principalmente.
Mediante SIMS se obtienen distribuciones laterales y en profundidad de la composición de cualquier elemento del sistema periódico en la muestra analizada, incluso es capaz de distinguir isótopos. La distinción es posible gracias al espectrógrafo de masas que distinge los elementos siempre y cuando sean partículas cargadas (Fig. 2.3).
Este sistema es capaz de medir [36] bajas concentraciones del orden de 1012 cm-3 y 1016 cm-3 dependiendo del elemento. Tiene por tanto una elevada sensibilidad. Para obtener buenos perfiles es preciso que:
Ya se ha comentado en la sección 1.2.1 las limitaciones de esta técnica.
Es una técnica no destructiva. Debe su nombre a Ernest Rutherford, quien en 1911 fue el primero en presentar el concepto de átomos que tienen núcleo. Cuando una muestra se bombardea con un haz de partículas de alta energía la gran mayoría de ellas queda implantada en el material. Esto es así porque el diámetro de núcleo atómico es del orden de 10-15 m mientras que el espacio entre los núcleos es del orden de 10-10 m. Una peque~na fracción de las partículas incidentes choca directamente con un núcleo intercambiando energía de forma elástica.
Se miden la energía y número de iones que se dispersan hacia atrás (backscattering) después de colisionar con los átomos cerca de la superficie de la muestra sobre la que se ha hecho incidir los iones. De esta manera es posible determinar la masa atómica y la concentración frente a la profundidad dentro de la muestra. Esta técnica está pensada para determinar la concentración de los elementos que son más pesados que los átomos constituyentes del própio sustrato. La sensibilidad para con los iones ligeros es muy pobre.
La energía medida para cada ángulo de salida depende de dos procesos: el frenado electrónico antes y después de la colisión que depende del material; y la energía intercambiada que depende de las masas de los átomos que intervienen (factor cinemático).
El número de sucesos de retrodispersión depende de dos factores: la concentración del elemento y del tama~no efectivo de su núcleo. La probabilidad de colisión se conoce como sección de captura (scattering cross section).
Se emplean típicamente iones ligeros, normalmente helio, de alta energía (1 a 5 MeV) que inciden perpendicularmente en la muestra. El detector de las partículas retrodispersadas se situa a casi 180 grados con respecto al haz incidente. Se registra la distribución de energías de los iones rebotados en esa dirección.
El factor cinemático Km se define como la relación entre la energía cinética del ion después y antes de la colisión:
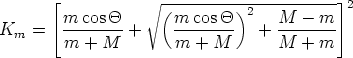 | (2.4) |
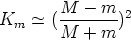 | (2.5) |
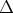 E = KmEincidente - Esalida estará directamente relacionada con la profundidad del
átomo blanco. El factor de conversión de energía a profundidad (
E = KmEincidente - Esalida estará directamente relacionada con la profundidad del
átomo blanco. El factor de conversión de energía a profundidad (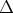 E = Sx) se calcula
aproximadamente como
E = Sx) se calcula
aproximadamente como
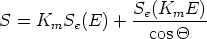 | (2.6) |
Es una técnica no destructiva y muy indirecta. Está basada en el cambio de las propiedades ópticas y térmicas del semiconductor debido al da~nado generado por la implantación ionica [93].
Se emplea principalmente como método de test en el proceso de fabricación de semiconductores [104]. Detecta las variaciones en las condiciones de implantación que afectan al da~nado generado y a la dosis implantada. Se puede usar para monitorizar cambios en la energía del haz de iones implantados, aunque su sensibilidad varía con la profundidad de penetración de los iones en el silicio. También es sensible al acanalamiento.
Las ondas térmicas se generan gracias a un haz láser modulado (1 MHz), también llamado láser de bombeo (Figura 2.4). Estas ondas se propagan con amortiguamiento crítico e interactuan con las características térmicas del material. En los materiales semiconductores aparecen ondas plasma de portadores libres producidas por el láser de bombeo. Las propiedades ópticas, como el índice de refracción, dependen de la temperatura de la muestra. La generación de ondas plasma y térmicas debidas al calentamiento periódico de la superficie de la muestra hacen que varíen de forma periódica las propiedades ópticas del material. Estas variaciones se detectan midiendo la reflectancia modulada de un haz laser que es reflejado por la superficie del material.
El láser de bombeo se enfoca en un punto de 1 micra de diámetro al igual que el haz láser
de sondeo. El haz reflejado tiene una componente alterna que es de la misma frecuencia que el
láser de bombeo. La se~nal TW que se mide es 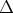 R/R que es adimensional y de dificil
interpretación.
R/R que es adimensional y de dificil
interpretación.
Permite monitorizar la implantación con baja dosis (1011 - 1012 iones/cm2) necesaria para controlar la tensión umbral de los transistores CMOS.
Las ventajas de esta técnica son:
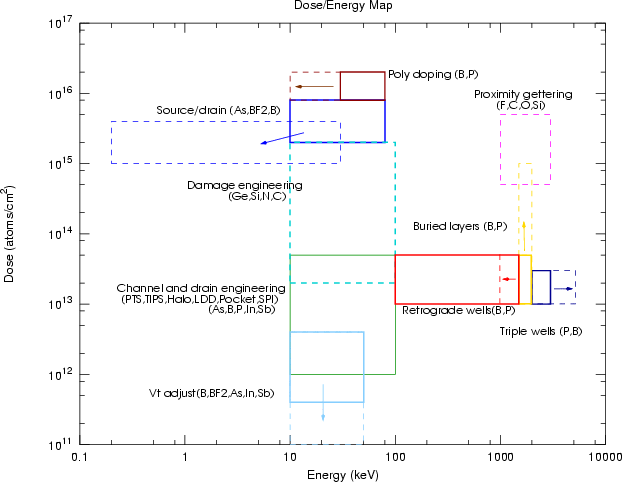
Actualmente existen tres tipos básicos de implantadores en las líneas de producción: alta corriente, corriente media y alta energía. Estos implantadores cubren todas las aplicaciones microelectrónicas. En la figura 2.5 se puede ver el rango de energías y dosis en los que se suele utilizar la implantación iónica para distintos tipos de aplicaciones [26]. En la actualidad el rango de aplicación se ha extendido en algunos casos (linea punteada). A continuación comentaremos brévemente algunas aplicaciones microelectrónicas y otras aplicaciones industriales de la implantación iónica.
|
Es la aplicación por excelencia de la implantación iónica. Es uno de los procesos clave en la fabricación de circuitos integrados VLSI y ULSI. Este proceso permite controlar con precisión el número de átomos implantados, la profundidad de los mismos y el perfil de impurezas ya que la implantación suele realizarse a temperatura ambiente y el tratamiento térmico posterior de las obleas también se realiza a temperaturas relativamente bajas. De esta manera se pueden obtener uniones muy superficiales, no dando pie a la difusión térmica de otras zonas previamente impurificadas.
Además proporciona una dispersión lateral muy peque~na lo que hace apropiado este proceso
para el dopado de regiones con dimensiones inferiores a 1 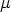 m.
m.
Es una de las primeras aplicaciones pensadas para la implantación iónica. La tensión umbral de un transistor MOSFET es:
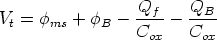 | (2.7) |
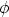 ms es la función trabajo metal-semiconductor,
ms es la función trabajo metal-semiconductor, 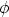 B es la barrera de potencial, Qf es la carga
fija del óxido, QB es una carga que depende del dopado del substrato y Cox es la capacidad del óxido
por unidad de área, es decir, Cox =
B es la barrera de potencial, Qf es la carga
fija del óxido, QB es una carga que depende del dopado del substrato y Cox es la capacidad del óxido
por unidad de área, es decir, Cox = 
 0/w, donde w es el espesor del óxido,
0/w, donde w es el espesor del óxido, 
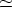 3.9 su constante
dieléctrica8
y
3.9 su constante
dieléctrica8
y  0 = 8.85 10-14 F/cm la permitividad del vacio.
Si se deposita una carga adicional QI justo entre el óxido y el semiconductor la tensión
umbral cambiará una cantidad:
0 = 8.85 10-14 F/cm la permitividad del vacio.
Si se deposita una carga adicional QI justo entre el óxido y el semiconductor la tensión
umbral cambiará una cantidad:
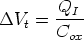 | (2.8) |
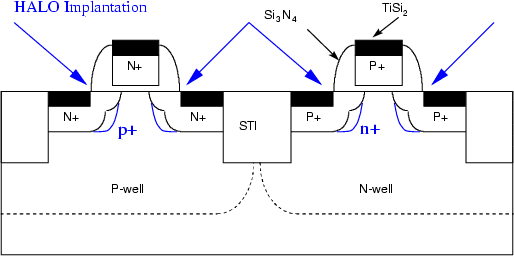
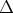 V t.
Cuando el máximo de la distribución de impurezas implantadas se encuentra entre la
interfase y el borde de la zona de carga espacial del semiconductor se pueden realizar
cálculos basados en la suposición de que la carga total implantada se encuentra a la
profundidad del centroide de la distribución. Sin embargo, la dosis necesaria se suele
determinar experimentalmente partiendo del valor aproximado obtenido en la ecuación
2.8.
V t.
Cuando el máximo de la distribución de impurezas implantadas se encuentra entre la
interfase y el borde de la zona de carga espacial del semiconductor se pueden realizar
cálculos basados en la suposición de que la carga total implantada se encuentra a la
profundidad del centroide de la distribución. Sin embargo, la dosis necesaria se suele
determinar experimentalmente partiendo del valor aproximado obtenido en la ecuación
2.8.
En esta aplicación se intentan corregir las tolerancias de la litografía y así optimizar las características de los dispositivos. En los transistores MOSFET la anchura del electrodo de puerta debe ser suficientemente grande como para alcanzar las regiones de fuente y drenador, pues de lo contrario no podría formarse un canal entre ellas y el transistor no funcionaría. El electrodo de puerta se fabricaba de forma que solapase parte de las regiones de la fuente y el drenador, pero esto introducía unas capacidades parásitas que reducían la frecuencia máxima de conmutación del transistor.
La solución consiste en utilizar un electrodo de puerta más estrecho que el canal. Una vez depositado el metal de la puerta se realiza una implantación a través del óxido de puerta que extiende las áreas de fuente y drenador hasta los bordes mismos del electrodo de puerta (figura 2.6), que sirve de máscara para la implantación. Si se usan puertas de polisilicio, la implantación permite además un dopado del mismo.
El gettering consiste en la eliminación de impurezas y defectos de las regiones de unión. La utilización de la implantación iónica para la eliminar impurezas de metales pesados se conoce desde hace algún tiempo [98]. El gettering necesita de tres efectos físicos:
La acumulación de un determinado tipo de átomos a una determinada profundidad, via implantación iónica u otras técnicas, hace que las impurezas superficiales se liberen y difundan hacia estas zonas profundas donde se aglomeran. En esta zona no son importantes los defectos o las impurezas eléctricamente, por lo que el dispositivo fabricado, que se encuentra en la superficie, funcionará correctamente.
Consiste en la formación de capas de materiales compuestos a una cierta profundidad dentro del semiconductor mediante la implantación de uno de los elementos. Así para formar una capa de SiO2 se implanta oxígeno en una oblea de silicio [75]. Las dosis necesarias son muy altas (1017 - 1018 cm-2), ya que se debe alcanzar una concentración de impurezas similar a la densidad atómica del substrato. Además, se necesita una corriente elevada del haz de iones (100 mA) para llevar la implantación a cabo en un tiempo razonable. Existen implantadores especiales de alta corriente en los que se suele suprimir la etapa de análisis del haz.
En estos casos se genera una capa de material amorfo, y se debe evitar que alcance la superficie, ya que sino será muy dificil reconstruir el silicio cristalino. Para reducir la amorfización de la superficie del silicio se realiza la implantación a temperaturas medias de 500oC. La capa enterrada de óxido o nitruro de silicio se obtiene tras un tratamiento térmico. Con esto conseguimos formar una capa enterrada de material aislante. La capa de silicio que queda en la superficie suele ser tan fina que no pueden fabricarse en ella dispositivos, por lo que se suele recurrir a un crecimiento epitaxial de la misma.
|
La solución a este problema es aumentar la impurificación del sustrato (ver figura 2.7), en las zonas de extensión de fuente y drenador. Esto se hace implantado con mucha inclinación y rotando cuatro veces la oblea en 90 grados para cubrir todos los lados del transistor. El dopado se hace con la misma especie con la que se impurificó el pozo (well).
El implante HALO junto con el implante del pozo determinarán la tensión umbral del transistor [16].
Recientemente se ha constatado que las propiedades mecánicas y/o químicas de algunos materiales mejoran cuando el material se implanta (impurifica) superficialmente con otros materiales.
Las propiedades mecánicas y químicas que se mejoran son, entre otras: la dureza (aceros implantados con Nitrógeno), la corrosión (implantación de Cr, Si, Ce), el desgaste, el pegado (los moldes metálicos de piezas plasticas se despegan más fácilmente al ser tratados), etc. Los materiales a los que se les somete al proceso suelen variar desde aceros, aleaciones de aluminio, de titanio, a plásticos, etc. Las implantaciones se realizan con energías de hasta 200 keV y con dosis muy altas (1018 átomos/cm2).
El concepto del implantador cambia al tratarse de tratamientos industriales para piezas mecanicas de gran tama~no (superfícies de 1 m2) y con dosis muy altas, que requieren ser procesadas en un tiempo razonable (rentable). Por ello se necesitan potencias muy altas y desenfocar el haz de iones para no volatilizar el material.
| Si todo parece estar yendo bien, |
| obviamente has pasado algo por alto |
| ~ Anonimo ~ |
Después de repasar la parte experimental de la implantación iónica ha llegado el momento de resumir las diferentes formas de abordar el problema de la simulación del proceso en la sección 3.2.
El método Monte Carlo, es un modelo estadístico básico que se utiliza en todas las formas de abordar el problema de la simulación. Consiste en seguir un número elevado de trayectorias seleccionadas aleatoriamente, de manera que al final se obtiene un histograma estadístico de los perfiles de implantación deseados. Existen algoritmos para reducir el ruido estadístico en estos histogramas, que al tiempo sirven para reducir el número de trayectorias que hay que simular para obtener un perfil simulado de impurezas aceptable. Estos algoritmos se estudian en la sección 3.3.
Cuando se quieren emplear los perfiles de impurezas obtenidos experimentalmente o por simulación en otros programas simuladores de dispositivos es necesario buscar una forma sencilla de representarlos utilizando unas distribuciones conocidas que ajusten el perfil utilizando un conjunto reducido de parámetros. Estas distribuciones se estudian en la sección 3.4.
En esta sección se hace una revisión de algunas de las técnicas de simulación empleadas para la resolución del problema de la implantación iónica.
Esta teoría no es própiamente una técnica de simulación si no más bien un planteamiento que por su sencillez hace de él, la primera técnica de simulación1. En los a~nos 60, Lindhard, Scharff y Schiott modelizaron [61, 62] de una forma sencilla el proceso de la implantación iónica dando lugar a la teoría que lleva sus iniciales. Las aproximaciones utilizadas limitan seriamente la precisión del modelo.
En esta teoría se consideran independientes los diferentes mecanismos de frenado de los iones y se calcula la pérdida energética por unidad de longitud como la suma
![[ ] [ ] [ ]
dE- = dE- + dE-
dx dx dx
total nuclear electronico](tesis19x.gif) | (3.1) |
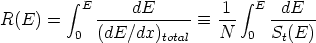 | (3.2) |
 en el sistema
centro de masas (ver figura 3.2 en la pagina 80), vale
en el sistema
centro de masas (ver figura 3.2 en la pagina 80), vale
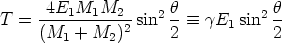 | (3.3) |
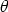 = 180 grados), la energía transferida T m = T (180 grados)
es máxima. El ángulo de dispersión se obtiene integrando la ecuación de movimiento utilizando
un potencial de interacción culombiano apantallado
= 180 grados), la energía transferida T m = T (180 grados)
es máxima. El ángulo de dispersión se obtiene integrando la ecuación de movimiento utilizando
un potencial de interacción culombiano apantallado
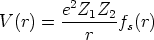 | (3.4) |
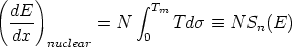 | (3.5) |
 es la sección de captura. La teoría LSS introduce una serie de variables reducidas que
hacen más tratables las integrales y que son
es la sección de captura. La teoría LSS introduce una serie de variables reducidas que
hacen más tratables las integrales y que son  (energía),
(energía), 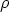 (distancia) y t (parámetro de
dispersión) definidos como sigue
(distancia) y t (parámetro de
dispersión) definidos como sigue 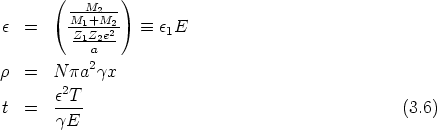
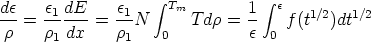 | (3.7) |
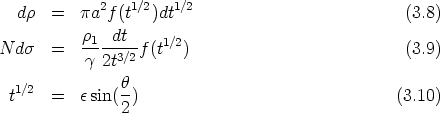
La función de dispersión f(t1/2) depende de la forma de V (r). El uso del apantallamiento de
Thomas-Fermi sobre el rango completo de valores de t proporciona una curva de pérdidas
energéticas nucleares d /d
/d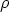 universal. Esta pérdida es independiente de Z1, Z2, M1, M2 y N.
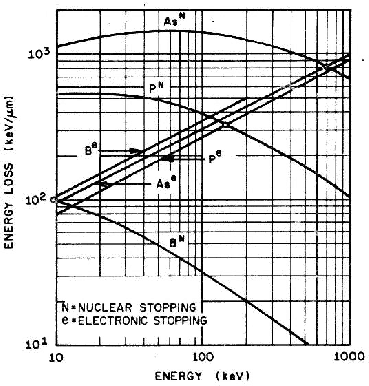
En general (ver figura 3.1), las pérdidas nucleares son relativamente peque~nas a altas energías
dado que las partículas rápidas disponen de menos tiempo para interaccionar, o lo que es lo
mismo, su sección de captura es menor. Para energías intermedias las pérdidas nucleares crecen,
y para energías más bajas donde la carga Z2 está apantallada la pérdida energética nuclear de
nuevo se reduce.
universal. Esta pérdida es independiente de Z1, Z2, M1, M2 y N.
En general (ver figura 3.1), las pérdidas nucleares son relativamente peque~nas a altas energías
dado que las partículas rápidas disponen de menos tiempo para interaccionar, o lo que es lo
mismo, su sección de captura es menor. Para energías intermedias las pérdidas nucleares crecen,
y para energías más bajas donde la carga Z2 está apantallada la pérdida energética nuclear de
nuevo se reduce.
El frenado electrónico en la teoria LSS es proporcional a la velocidad del ion
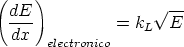 | (3.11) |
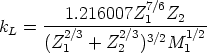 | (3.12) |
En la figura 3.1 se dibujan las curvas de frenado nuclear y electrónico para diversos iones implantados en función de la energía incidente de los mismos. Hay que hacer notar que la suma de ambas pérdidas energéticas es aproximadamente constante en un cierto rango de energías.
|
A partir de los valores del frenado se obtiene el rango proyectado
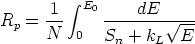 | (3.13) |
La simulación de la implantación ionica utilizando la aproximación de colisiones binarias (BCA) se enmarca dentro del método Monte Carlo. En él, se siguen las trayectorias individuales de un gran número de iones tomando de forma aleatoria las condiciones de partida (posición, velocidad). El perfil de impurezas se obtiene calculando el histograma de las posiciones finales de los iones en el material.
La aproximación de colisiones binarias consiste en que al seguir la trayectoria del ion o de cualquier átomo puesto en movimiento, se considera que sólo se colisiona con el átomo más cercano cada vez. Es decir, en las colisiones sólo intervienen dos partículas. El proyectil perderá, parte de su energía cinética de forma elástica transmitiendosela al blanco, y parte, de forma inelástica interactuando con los electrones del medio a medida que avanza por este. Cuando la energía cinética del proyectil sea inferior a una energía umbral dada (ET ), se considerará que el ion se ha parado.
Si la energía transferida a un átomo blanco es superior a la energía de enlace (Eb) del mismo con la red cristalina, entonces este átomo será seguido como proyectil secundario. Esto permite llevar cuenta del da~nado, vacantes, intersticiales, etc., generados en una cascada de colisiones.
Dependiendo de si el material blanco es cristalino o amorfo se han desarrollado dos modelos para tratar el problema usando la misma aproximación BCA.
El programa de simulación TRIM (TRansport of Ions in Matter) fue desarrollado por Ziegler, Biersack y Littmark [118] y sólo permite implantaciones en materiales amorfos. Coincide aceptablemente bien con el experimento. Es un programa de cálculo rápido. Utiliza el concepto de recorrido libre medio para la generación aleatoria de átomos blanco y, el cálculo de las pérdidas electrónicas se hace mediante funciones ajustadas a datos experimentales. En la resolución de las colisiones nucleares emplea una aproximación numérica conocida como fórmula mágica para el cálculo de los ángulos de dispersión.
Frenado nuclear. Después de aplicar los principios de conservación de energía y momento a la
colisión binaria, el problema se reduce a conocer cual es el ángulo de dispersión 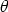 formado por las asíntotas de las trayectorias del proyectil y el blanco en el sistema de
referencia centro de masas. La fórmula mágica es un ajuste de las soluciones de la
ecuación
formado por las asíntotas de las trayectorias del proyectil y el blanco en el sistema de
referencia centro de masas. La fórmula mágica es un ajuste de las soluciones de la
ecuación
![integral oo [ ]-1
Q = p - 2p dr r2g(r)
R](tesis31x.gif) | (3.14) |
En la figura 3.2 se representa la colisión entre dos partículas en el sistema de referencia
centro de masas. Se aprecia el llamado triángulo de dispersión, uno de cuyos vértices forma un
ángulo de 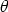 /2, cumpliendo
/2, cumpliendo
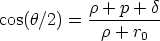 | (3.15) |
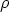 =
= 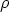 1 +
1 + 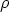 2,
2, 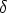 =
= 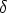 1 +
1 + 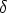 2, p es el parámetro de impacto y
2, p es el parámetro de impacto y 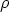 1 y
1 y 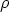 2 los radios de curvatura
de las trayectorias del proyectil y blanco respectivamente, en el punto de máxima aproximación
o ápside. La distancia en ese punto es r0. Los valores
2 los radios de curvatura
de las trayectorias del proyectil y blanco respectivamente, en el punto de máxima aproximación
o ápside. La distancia en ese punto es r0. Los valores 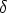 1 y
1 y 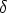 2 son términos de corrección (Ver
fig. 3.2).
La distancia r0 se obtiene de la resolución numérica de la ecuación [66]
2 son términos de corrección (Ver
fig. 3.2).
La distancia r0 se obtiene de la resolución numérica de la ecuación [66]
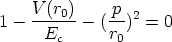 | (3.16) |
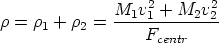 | (3.17) |
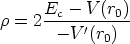 | (3.18) |
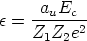 | (3.19) |
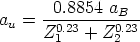 | (3.20) |
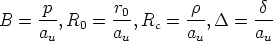 | (3.21) |
La ecuación 3.15 queda
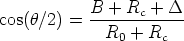 | (3.22) |
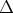 , que es el término de corrección cuyo ajuste se corresponde
con las ecuaciones siguientes [118]:
, que es el término de corrección cuyo ajuste se corresponde
con las ecuaciones siguientes [118]: 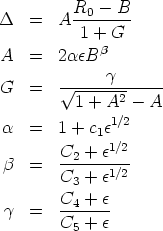
Para altas energías se emplea un potencial Culombiano en vez del potencial ZBL siendo el cálculo del ángulo de dispersión mucho más simple
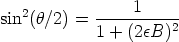 | (3.23) |
Recorrido libre medio. En TRIM sólo se puede implantar en materiales amorfos en los que
los átomos se encuentran aleatoriamente distribuidos cumpliendo que la densidad promedio
coincida con la del material. En el caso del silicio amorfo vale 5 * 1022 átomos/cm3. En el
programa se generan aleatoriamente los átomos cuando el ion ha recorrido una determinada
distancia L llamada recorrido libre medio. Esta distancia se escoge como la distancia que ha de
recorrer el ion para tener una colisión fuerte que le provoque una desviación angular
grande (> 5 grados) ignorando todas las demás colisiones suaves. Con esto se consigue
reducir el tiempo de cálculo considerablemente, sobre todo en las implantaciones a alta
energía.
Consideremos la probabilidad de encontrar un blanco con un parámetro de impacto
comprendido entre p y p + 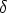 p a lo largo de la trayectoria L:
p a lo largo de la trayectoria L:
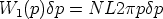 | (3.24) |
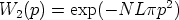 | (3.25) |
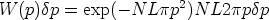 | (3.26) |
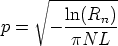 | (3.27) |
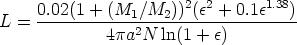 | (3.28) |
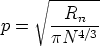 | (3.29) |
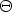 en el sistema de referencia del laboratorio. En este sistema:
en el sistema de referencia del laboratorio. En este sistema:
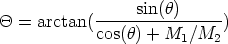 | (3.30) |
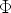 = 2
= 2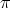 Rn),
donde Rn es un nuevo número aleatorio entre 0 y 1.
Finalmente la energía transferida elásticamente al blanco será:
Rn),
donde Rn es un nuevo número aleatorio entre 0 y 1.
Finalmente la energía transferida elásticamente al blanco será:
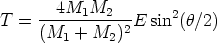 | (3.31) |
Frenado electrónico. En principio suponemos que las pérdidas electrónicas no están relacionadas con las nucleares. Entonces, la pérdida de energía entre dos colisiones sucesivas podría valer
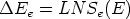 | (3.32) |
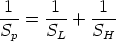 | (3.33) |

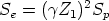 | (3.35) |
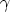 representa la fracción de carga efectiva del ion, que tiene en cuenta el
apantallamiento del núcleo debido a los electrones, y que depende de la fracción de carga
real q del ion, esto es, su grado de ionización.
Para estimar q se recurre al criterio de Bohr, según el cual el proyectil pierde los
electrones cuya velocidad orbital sea menor que la velocidad relativa entre el ion y los
electrones del blanco que vale:
representa la fracción de carga efectiva del ion, que tiene en cuenta el
apantallamiento del núcleo debido a los electrones, y que depende de la fracción de carga
real q del ion, esto es, su grado de ionización.
Para estimar q se recurre al criterio de Bohr, según el cual el proyectil pierde los
electrones cuya velocidad orbital sea menor que la velocidad relativa entre el ion y los
electrones del blanco que vale: 
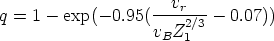 | (3.38) |
![[ ]
( 4/\vf-)2
g = q + C(1 - q) ln 1 + a v
B B](tesis57x.gif) | (3.39) |
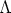 el radio de apantallamiento del ion definido como
el radio de apantallamiento del ion definido como
![---2aB(1---q)2/3---
/\ = 1/3
Z1 [1 - (1 - q)/7]](tesis58x.gif) | (3.40) |
Para energías bajas donde el frenado electrónico es proporcional a la velocidad, sí puede existir una fuerte correlación entre el frenado nuclear y el electrónico. En TRIM está implementado el modelo de Oen-Robinson [77]
Es un modelo de frenado electrónico [88, 87, 86, 47] local. La energía perdida será
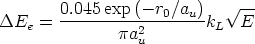 | (3.41) |
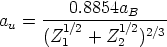 | (3.42) |
Utilizando la misma aproximación de colisiones binarias descrita en la sección anterior, el problema es ahora simular la implantación iónica en materiales cristalinos en las que el material presenta canales (ver figura 4.4 en la página 157) y el comportamiento de los proyectiles en su interior no es isótropo.
MARLOWE fue el primer programa que utilizó esta metodología y fue desarrollado por Robinson et al. [47, 77, 86, 87, 88], aunque ha dado lugar a multitud de versiones y modificaciones como UT-MARLOWE [55, 56, 54, 71, 72, 78, 79, 100, 112, 114, 113, 115], o incluso una versión UVA-MARLOWE desarrollada en la Universidad de Valladolid [2, 4, 5, 49, 50].
En esta aproximación y al contrario que en TRIM se busca una representación lo más detallada posible de lo que ocurre dentro del cristal, sin olvidar nunca la grosera aproximación de las colisiones binarias, que limitará el rango de aplicación de los programas.
El hecho de tener que describir el material cristalino complica mucho su programación. Será necesario hacer uso de las propiedades traslacionales de la red para obtener las posiciones de los blancos próximos al proyectil3. Existirá por tanto un mecanismo de búsqueda de blancos próximos al proyectil, que tendrá en cuenta vacantes e intersticiales existentes con anterioridad. Esto permite simular la implantación en un material con defectos cristalinos.
Aproximación cuasielástica: colisiones nucleares. Esta aproximación tiene en cuenta las pérdidas electrónicas asociadas a las colisiones a la hora de evaluar la energía de salida y los ángulos de dispersión4. Además se cuenta con una corrección para mejorar las trayectorias en situaciones muy simétricas donde se interacciona con más de un átomo a la vez, es lo que se conoce como extensión de colisiones múltiples [87, 77].
En una colisión, el ángulo de dispersión en el sistema centro de masas se calcula resolviendo:
![integral
oo [2 ]-1
Q = p - 2p R dr r g(r)](tesis61x.gif) | (3.43) |
![[ p2 (1 + A)V (r)]1/2
g(r) = 1- ---- ------------
r2 AE1](tesis62x.gif) | (3.44) |
El potencial interatómico implementado en el programa es el potencial de Moliere [70] que vale:
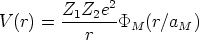 | (3.45) |
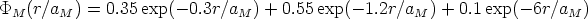 | (3.46) |
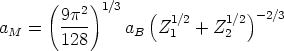 | (3.47) |
Modelo de frenado electrónico Las pérdidas inelásticas tienen dos contribuciones, que pueden ser o no aplicadas conjuntamente.
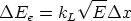 | (3.48) |
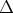 x es la distancia recorrida por el ion, E su energía cinética, y
x es la distancia recorrida por el ion, E su energía cinética, y
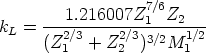 | (3.49) |
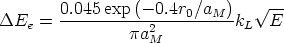 | (3.50) |
Modelo de colisiones simultáneas Este modelo es una corrección para mejorar aquellas colisiones en las que no es posible determinar una secuencia de colisiones, como pueda ser cuando el ion esté en condiciones de acanalamiento. En estos casos se calculan la colisión simultánea utilizando la siguiente aproximación:
Esta aproximación grosera permite que los iones no se desacanalen, aunque tiene el inconveniente de introducir un error sistemático en las energías de salida, aunque no es muy grande, y el porcentaje de colisiones de este tipo sólo será importante en condiciones de acanalamiento (p. ej. canal {110} en el silicio).
Mecánica de funcionamiento El programa es capaz de seguir la trayectoria del proyectil y de los proyectiles secundarios hasta que se paren. Se considerará que un ion está parado cuando su energía cinética esté por debajo de un determinado umbral Et. Se generará un proyectil secundario cuando al colisionar con un átomo de la red cristalina, se le transmita una cantidad de energía, T , mayor que la energía de enlace, Eb, con la red. Después se seguirá la trayectoria del proyectil secundario con una energía cinética E = T - Eb. Se siguen todas las trayectorias de todos los proyectiles hasta que se paran.
La diferencia fundamental con respecto a la simulación BCA está en una descripción detallada de prácticamente todos los átomos del cristal y del ion, tanto de su posición como de su velocidad, estudiando las interacciones de cada átomo sobre todos los demás. Esto se traduce en un considerable aumento del tiempo de cálculo, lo que restringe el uso de estas simulaciones a casos sencillos, como implantaciones de baja energía, aunque a cambio se obtiene una información muy detallada y precisa de lo que está ocurriendo.
Este método se basa en la resolución de las ecuaciones de movimiento de un sistema grande de partículas5. Este conjunto de ecuaciones se discretizan para poder ser resueltas mediante algún algoritmo numérico en un computador. Las ecuaciones diferenciales para cada partícula se pueden escribir como:
donde se suponen fuerzas conservativas que dependen de la posición de las partículas, aunque en algunos casos sea necesario incluir fuerzas viscosas que disipen energía y que dependerán por lo general de la velocidad de las partículas oponiendose al movimiento de las mismas. La fuerza que actua sobre cada partícula se obtiene de la energía potencial del sistema. En
principio, dependerá de las coordenadas de todas las partículas U = U(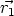 ,
, 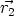 , ..,
, .., 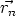 ), y se
calculará como:
), y se
calculará como:
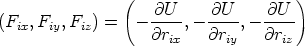 | (3.52) |
La precisión de estos algoritmos depende del orden de los mismos y del paso temporal empleado. Dependiendo de la duración de los procesos a simular hay que tomar un paso temporal u otro. Si la evolución de las partículas es lenta, se escogerá un paso temporal grande y se podrá simular un tiempo total grande. Si por el contrario la velocidad es alta, habrá que tomar un espaciado temporal peque~no para evitar errores en el cálculo de las trayectorias. La mejor solución estará en coger un paso ajustable que se adapte a las circunstancias de la simulación. Se suele utilizar h = k/V M donde V M es la máxima velocidad del conjunto de partículas en el paso temporal anterior [41].
El orden del algoritmo predictor-corrector nos indicará el número de pasos como el anterior, necesarios para dar como válida una solución. Un orden alto del algoritmo aumenta la exactitud, pero necesita mayor tiempo de cálculo y una mayor cantidad de memoria en el computador.
Dentro de los algoritmos más sencillos se encuentra el de Verlet, de orden 2. Con ordenes mayores tenemos los de Gear, Beeman, y Adams-Moulton [22, 41].
El resultado de la simulación depende fuertemente de la energía potencial del sistema. Aunque en un caso general la energía potencial depende de las posiciones de las partículas, es conveniente hacer algunas simplificaciones. Si suponemos que el potencial en un punto depende solo de las distancias a las partículas que forman el sistema, tendremos:
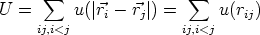 | (3.53) |
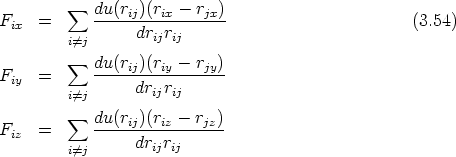
La fuerza, para un sistema real de partículas, deberá cumplir que sea atractiva cuando las partículas se separen y que sea repulsiva cuando se acerquen demasiado. El potencial que obedece a este comportamiento tendrá un mínimo en la distancia de separación interatómica del sólido.
El potencial de Lennard-Jones (figura 3.3) responde a este comportamiento:
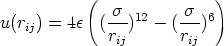 | (3.55) |
 y
y  son los parámetros de ajuste del potencial. Sin embargo, un potencial entre dos
cuerpos no permite la simulación de sólidos cristalinos covalentes, ya que no depende de la
orientación de las partículas. Tan sólo las redes cristalinas compactas se podrán representar
bien con este tipo de potenciales. Para los semiconductores de interés serán necesarios
potenciales más complejos.
A continuación revisaremos los potenciales más extendidos para los cálculos de dinámica
molecular: Stillinger-Weber [96] y Tersoff [101, 103, 102]
son los parámetros de ajuste del potencial. Sin embargo, un potencial entre dos
cuerpos no permite la simulación de sólidos cristalinos covalentes, ya que no depende de la
orientación de las partículas. Tan sólo las redes cristalinas compactas se podrán representar
bien con este tipo de potenciales. Para los semiconductores de interés serán necesarios
potenciales más complejos.
A continuación revisaremos los potenciales más extendidos para los cálculos de dinámica
molecular: Stillinger-Weber [96] y Tersoff [101, 103, 102]
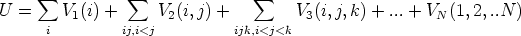 | (3.56) |
Dado que la estructura cristalina del silicio está compuesta por fuertes enlaces covalentes en
determinadas direcciones, parece lógico incluir al menos las contribuciones para dos y tres
cuerpos. Para simplificar el tratamiento se introducen unas unidades para escalar la energía ( )
y la distancia (
)
y la distancia ( )
)
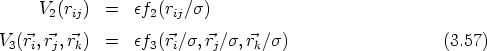
 y
y  de forma que el mínimo de f2 = -1 y f2(21/6) = -1. La función f
2 dependerá
sólo de la distancia entre las partículas, mientras que f3 debe poseer simetría rotacional para
representar la estructura tetraédrica del silicio.
de forma que el mínimo de f2 = -1 y f2(21/6) = -1. La función f
2 dependerá
sólo de la distancia entre las partículas, mientras que f3 debe poseer simetría rotacional para
representar la estructura tetraédrica del silicio.
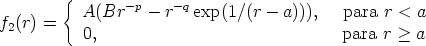 | (3.58) |
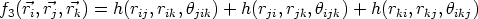 | (3.59) |
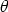 jik es el ángulo subtendido por los vectores
jik es el ángulo subtendido por los vectores 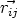 y
y 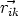 , y la función h tiene la forma:
, y la función h tiene la forma:
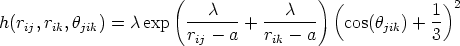 | (3.60) |
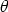 t tales que cos(
t tales que cos(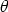 t) = -1/3. Este
ángulo coincide con el que forman los enlaces en los átomos de silicio en una red tipo
diamante.
t) = -1/3. Este
ángulo coincide con el que forman los enlaces en los átomos de silicio en una red tipo
diamante.Los parámetros ajustables de los potenciales se escogen [96] para que la red tipo diamante sea
la más estable y la temperatura de fusión coincida con la experimental (1683 K para el silicio).
Así A = 7.049556277, B = 0.6022245584, p = 4, q = 0, a = 1.80, 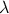 = 21.0 y
= 21.0 y 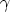 = 1.20. Los
factores de escala para la longitud
= 1.20. Los
factores de escala para la longitud  = 2.0951 Å y la energía
= 2.0951 Å y la energía  = 50 Kcal/mol = 2.167
eV.
= 50 Kcal/mol = 2.167
eV.
El potencial Stillinger-Weber descrito representa adecuadamente las fases cristalina y líquida del silicio, pero no es capaz de describir de forma adecuada el estado amorfo del silicio.
Este potencial está basado en la idea de que la fuerza de los enlaces existentes en un átomo depende de la disposición y número de átomos que le rodean. Básicamente es un potencial de dos cuerpos, pero corregido mediante unos factores que tienen en cuenta la coordinación de cada partícula.
La energía potencial del sistema U puede descomponerse en energías asociadas a las partículas Ei o asociadas a los enlaces V ij según convenga:
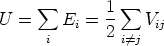 | (3.61) |
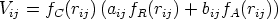 | (3.62) |

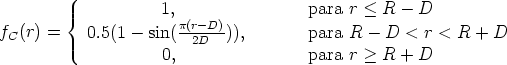 | (3.64) |
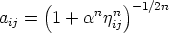 | (3.65) |
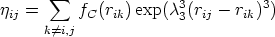 | (3.66) |
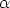 = 0 y por consiguiente aij = 1.
= 0 y por consiguiente aij = 1.
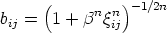 | (3.67) |
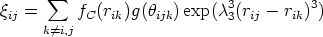 | (3.68) |
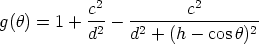 | (3.69) |
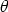 ijk el ángulo que forman los enlaces i-j e i-k.
El termino
ijk el ángulo que forman los enlaces i-j e i-k.
El termino 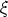 ij actúa como coordinación efectiva, y depende de la longitud de los enlaces y
de la orientación de los mismos. Como consecuencia bij
ij actúa como coordinación efectiva, y depende de la longitud de los enlaces y
de la orientación de los mismos. Como consecuencia bij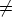 bji.
bji.Tersoff [101, 103, 102] ha definido tres potenciales para el silicio. El primero (T1) no se ajusta al modelo descrito y presenta algunas deficiencias. Los parámetros para los potenciales T2 y T3 aparecen en la figura 3.4. El que representa mejor al silicio en todas sus fases es el potencial T3.
|
Aún con estas aproximaciones y otras más el método es implicitamente lento. Viene a ser de dos a tres órdenes de magnitud más lento que la aproximación BCA. Cuando aumente la potencia computacional en varios órdenes de magnitud, será entonces el momento de utilizar dinámica molecular en la simulación de casi todos los procesos tecnológicos, ya que describe con más precisión lo que ocurre.
Se pretende conseguir una solución analítica de la distribución de átomos implantados. Para ello se buscarán los momentos de una distribución Pearson IV (ver sección 3.4). Sin embargo, la complejidad de los frenados elástico e inelástico, hará que sólo se puedan obtener soluciones mediante el cálculo numérico.
El planteamiento del problema consiste en encontrar la función F (x) que describa la
probabilidad de que un ion agote su energía cinética en un rango de profundidades (x, x + dx).
Es lógico presuponer que esta probabilidad dependerá de la energía inicial de los
iones y de su dirección con respecto a la superficie del blanco F (x, E, 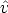 ). En un caso
tridimensional, la función F dará la probabilidad de que el ion se detenga en un
elemento de volumen d3r situado en la posición
). En un caso
tridimensional, la función F dará la probabilidad de que el ion se detenga en un
elemento de volumen d3r situado en la posición 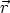 . Entonces la función F depende de
F (
. Entonces la función F depende de
F (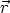 , E,
, E, 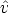 ).
).
Para poder abordar el cálculo necesitamos hacer algunas simplificaciones:
Las colisiones elásticas entre el ion y los átomos del blanco se describen a través de la sección
de captura d n(E, T n,
n(E, T n, 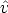 ,
, 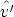 ) para cambiar el estado del ion desde (E,
) para cambiar el estado del ion desde (E, 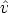 ) hasta (E - T n,
) hasta (E - T n, 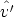 ),
donde T n es la energía transferida al átomo blanco y
),
donde T n es la energía transferida al átomo blanco y 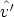 es la dirección de salida del ion tras la
colisión.
es la dirección de salida del ion tras la
colisión.
Las pérdidas inelásticas se producen de forma contínua y no cambian la dirección del ion.
Su sección de captura es d e(E, T e), donde T e es la energía transferida a los electrones del
blanco.
e(E, T e), donde T e es la energía transferida a los electrones del
blanco.
Las secciones de captura se calculan con un modelo similar al empleado en la Teoría LSS. La ecuación de transporte de Boltzman que describe los procesos mencionados será:
donde cos(
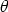 ) aparece como consecuencia del movimiento del ion en direcciones no
perpendicualres a la superficie, y N es el número de iones.
) aparece como consecuencia del movimiento del ion en direcciones no
perpendicualres a la superficie, y N es el número de iones.
Una manera de resolver la ecuación de forma numérica es utilizar un método
Monte Carlo [39]. La función de distribución del momento se representa con una
matriz bidimensional F ij, donde cada elemento se corresponde con las partículas con
una energía Ei(0 < Ei < E0) moviendose en la dirección 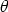 i(
i(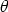 i <
i < 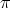 /2) (Ver figura
3.5).
/2) (Ver figura
3.5).
En un estado inicial la distribución de momentos en el plano de la superficie es
una función delta, 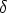 (E0,
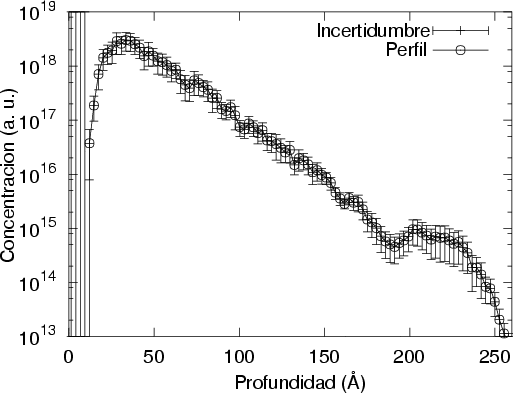
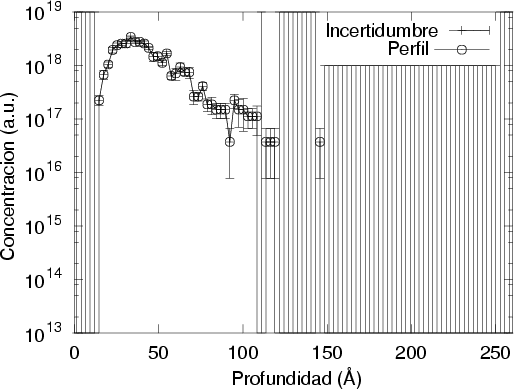
(E0, 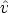 ), dada por la energía de los iones E0 y su dirección. El
momento puede ser sustitudo por su energía E y el ángulo
), dada por la energía de los iones E0 y su dirección. El
momento puede ser sustitudo por su energía E y el ángulo 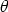 si nos encontramos en un
plano6.
En cada paso del cálculo, la redistribución de las partículas en el espacio de momentos para una
profundidad x y en un elemento dx se obtiene resolviendo la ecuación 3.70. Cuando los
iones tengan una energía por debajo de un límite establecido Emin se considerarán
parados y se almacenarán en el histograma correspondiente a la profundidad x (ver
figura 3.6). El resto de iones continuarán moviendose hasta que pierdan la energía
necesaria.
si nos encontramos en un
plano6.
En cada paso del cálculo, la redistribución de las partículas en el espacio de momentos para una
profundidad x y en un elemento dx se obtiene resolviendo la ecuación 3.70. Cuando los
iones tengan una energía por debajo de un límite establecido Emin se considerarán
parados y se almacenarán en el histograma correspondiente a la profundidad x (ver
figura 3.6). El resto de iones continuarán moviendose hasta que pierdan la energía
necesaria.
Este método es utilizado en programas como SUPREM IV [90] para la simulación de implantaciones en materiales amorfos. Utilizan una resolución numérica, similar a la citada, de la ecuación de transporte.
La generación de un perfil de implantación ya sea en una dimensión o en varias es un proceso estadístico donde los sucesos más probables, los situados en el punto máximo del perfil, tienen menos ruido estadístico y están representados con mas precisión. Sin embargo, los sucesos menos probables (rare events) quedan representados con un alto nivel de ruido, que hace que no se pueda decir con precisión dónde acaba o dónde comienza el perfil de impurezas con respecto al nivel de fondo del material implantado. Para poder mejorar la representación de este tipo de sucesos poco probables se han desarrollado varios algorítmos (rare event algorithm [114, 12, 8]) de mejora estadística.
|
Estos algorítmos consisten, básicamente, en identificar los sucesos poco probables y simular varias veces el comportamiento de este suceso partiendo del mismo punto y siguiendo trayectorias ligeramente diferentes, dando un peso estadístico ponderado a cada una de las simulaciones. De esta manera conseguimos reducir el ruido estadístico al haber aumentado el número de simulaciones para el caso poco probable (Ver figura 3.7).
Han sido varios los autores que han descrito posibles mecanísmos de identificación y mejora de sucesos poco probables relacionados con el tema de la implantación iónica. Sin embargo, estas técnicas han aparecido en muchas otras disciplinas científicas [48] y tecnológicas [40] para mejorar las simulaciones en determinadas circunstancias.
La segunda etapa consiste en utilizar la lista anteriormente generada para simular varias trayectorias de iones que parten del plano d1 para cada ion de la lista. Cuando los iones superan la profundidad d2 se procede a almacenar de nuevo la información necesaria de los iones para repetir el proceso varias veces. Se almacena el segundo trozo de perfil y se continúa.
Se obtienen cascadas diferentes gracias a que las posiciones de los átomos del cristal son aleatorias debido a la vibración térmica del mismo, que es también simulada. Se consigue de esta manera un doble objetivo, mejorar la precisión en profundidad de los perfiles unidimensionales y mejorar el tiempo de cálculo ya que las cascadas se calculan de forma parcial.
Sin embargo, el algoritmo presentado por Yang et al. adolece de algunos problemas, como el de no estar integrado en el programa de simulación siendo necesarias varias etapas de cálculo independientes con almacenamientos intermedios, además de no tener optimizado, en manera alguna, el tiempo de cálculo, que puede incluso ser mayor que sin el algoritmo, y el número de repeticiones de las últimas subtrayectorias de las cascadas. Tampoco incluye ninguna regla clara de como escoger las profundidades di, que suponemos responderán a un conocimiento previo del resultado.
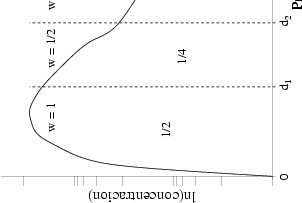
La forma característica de un perfil típico se muestra en la figura 3.8. Tiene un máximo cerca de la superficie seguido de una caida exponencial. La concentración de impurezas en la cola del perfil es varios órdenes de magnitud menor que en el máximo. Para obtener la misma precisión estadística para todas las profundidades debemos simular muchos iones que quedarán en el pico para cada uno que se pare en la cola. La mayor parte del esfuerzo computacional no redundará en mejorar la estadística de la cola.
|
Para reducir este cálculo innecesario se emplea un esquema de subdivisión de los átomos (atom splitting) que incrementa el muestreo para las zonas más profundas del perfil. Cada ion es reemplazado por varios iones virtuales, cada uno con un peso estadístico asociado. A ciertas profundidades, cada ion se reemplaza por dos iones, cada uno de ellos con la mitad del peso estadístico anterior a la subdivisión.
La trayectoria de cada ion virtual se sigue de forma individual, subdividiendolo sucesivas veces. Como los átomos que rodean al ion virtual se encuentran en un estado diferente cada vez7 conseguimos trayectorias diferentes. De este manera, se puede mantener el mismo número de iones virtuales para cada profundidad, aunque los pesos decrecen con ella.
Para optimizar las ventajas de este esquema, se actualizan dinámicamente las profundidades de subdivisión. La distribución inicial de profundidades de subdivisión está tomada en base a un perfil de impurezas estimado para las condiciones de implantación. Una vez que comienza la simulación, las profundidades de subdivisión son reevaluadas cada cierto número de cascadas.
Al principio de la simulación se especifíca el número de órdenes de magnitud, M, de concentración de iones sobre los que se desea mejorar el perfil (Fig. 3.8). Se dividen los iones cuando se alcanzan profundidades en las que el número total de iones, ignorando el peso estadistico, es la mitad del número actual de iones implantados. Se utilizan N profundidades de subdivisión (splitting depths), donde N es el entero más grande < M log 2(10). Las profundidades de subdivisión Di(1 < i < N) se escogen de forma que
![integral di 1 integral oo
C(x)dx = [1- (-)i] C(x)dx
0 2 0](tesis111x.gif) | (3.71) |
|
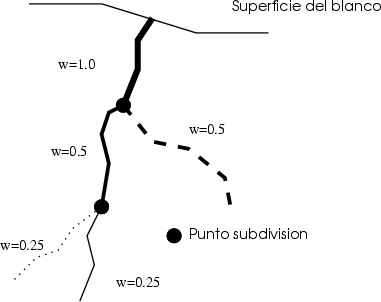
En cada punto se calcula Cloc/Cmax_current donde Cmax_current es la concentración global máxima y se compara con unos niveles de concentración relativos (0.3, 0.09, 0.027, .., (0.3)10). Se define un punto de división de trayectorias (trayectory split point) si la concentración local actual cae por debajo del nivel precedente.
Se almacenan entonces la posición, energía y velocidad para desarrollar posteriormente las ramificaciones virtuales de las trayectorias partiendo del punto de división del átomo. En cada division se genera un ion virtual que no vuelve a ser subdividido. A cada ion virtual se le asigna un peso estadístico mitad del anterior (ver figura 3.9).
Las desventajas de este modelo están en la complejidad que requiere mantener un árbol octal (octree) de concentraciones que cubra toda la zona de interés, el conocimiento a priori de valores como el número máximo de colisiones por trayectoria o la concentración global máxima. También se aprovechan poco las posibilidades de la subdivisión sucesiva de las trayectorias virtuales, que no son subdivididas de nuevo.
Desde los comienzos de la implantación iónica se ha buscado una forma sencilla, con pocos parámetros, de describir los perfiles de impurezas obtenidos. Para ello se han utilizado unas distribuciones estadísticas que se ajustan más o menos bien a los perfiles experimentales.
En esta distribución hay dos parámetros, el alcance previsto, RP que es el valor medio de la
profundidad de los iones implantados y la desviación cuadrática media 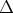 RP , que se definen
como:
RP , que se definen
como:
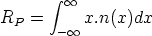 | (3.72) |
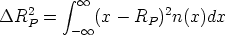 | (3.73) |
![[ 2]
n(R) = n0(RP )exp - (R---RP-)--
2DR2P](tesis115x.gif) | (3.74) |
Permite describir el perfil a partir de cuatro parámetros o ”momentos”: el alcance previsto RP ,
la desviación cuadrática media 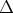 RP , la asimetría (skewness) que es nula para la distribución
gaussiana y la curvatura (kurtosis), que toma de valor 3 para la distribución anterior. Estos
parámetros o momentos se definen como sigue:
RP , la asimetría (skewness) que es nula para la distribución
gaussiana y la curvatura (kurtosis), que toma de valor 3 para la distribución anterior. Estos
parámetros o momentos se definen como sigue:
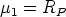 | (3.75) |
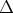 RP ). Se define el momento:
RP ). Se define el momento:
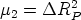 | (3.76) |
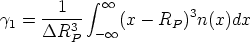 | (3.77) |
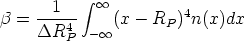 | (3.78) |
Y la distribución Pearson IV se define como:
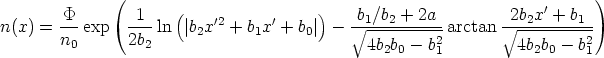 | (3.79) |

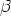 - 12
- 12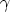 12 - 18,
12 - 18, 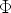 es la dosis de implantación y n0 la constante de normalización
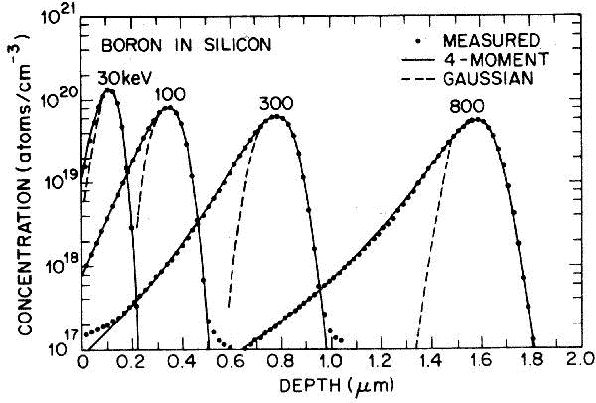
de la función Pearson IV en el rango de los datos experimentales. En la figura 3.10 se muestra
el resultado de ajustar unos puntos experimentales con una distribución gausiana y con una
distribución Pearson IV. Se observa claramente que la distribución Pearson IV se ajusta mejor
al comportamiento de los datos experimentales. Otro ejemplo se ve en la figura 3.11 donde la
distribución Pearson IV ajusta perfectamente unos datos experimentales [46] de implantación
de boro en silicio amorfo.
es la dosis de implantación y n0 la constante de normalización
de la función Pearson IV en el rango de los datos experimentales. En la figura 3.10 se muestra
el resultado de ajustar unos puntos experimentales con una distribución gausiana y con una
distribución Pearson IV. Se observa claramente que la distribución Pearson IV se ajusta mejor
al comportamiento de los datos experimentales. Otro ejemplo se ve en la figura 3.11 donde la
distribución Pearson IV ajusta perfectamente unos datos experimentales [46] de implantación
de boro en silicio amorfo.
|
Esta distribución está compuesta por una suma ponderada de dos distribuciones Pearson IV.
Es la mejor forma de describir perfiles con acanalamiento. Cada distribución Pearson representa
un mecanismo distinto: dispersion aleatoria, f(x), y acanalamiento, g(x). Esta distribución
tiene 9 parámetros ajustables que pueden ser calculados [79] utilizando el algoritmo
de Levenberg-Marquardt usando una combinación del método del gradiente y el
método de Gauss-Newton. Cada distribución Pearson tiene cuatro parámetros, y el
noveno, 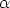 , representa la fracción de dosis para cada distribución. Se ha de cumplir que:
, representa la fracción de dosis para cada distribución. Se ha de cumplir que:
![integral oo
DT = [af (x) + (1- a)g(x)]dx
0](tesis124x.gif) | (3.81) |
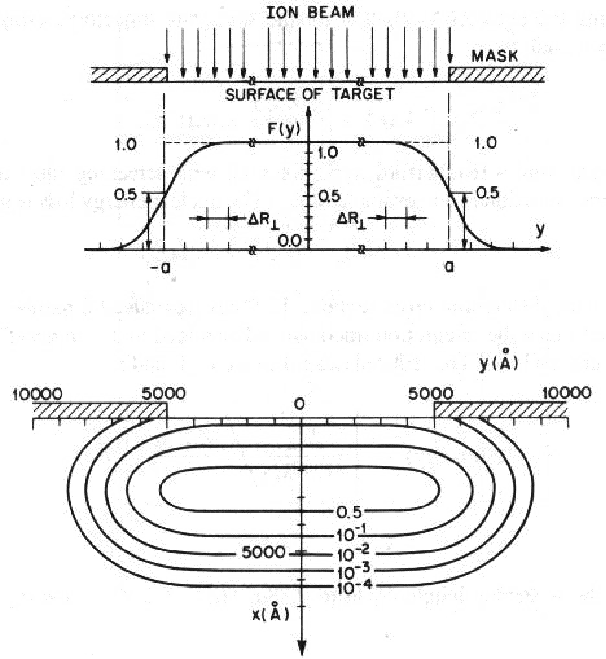
Actualmente interesa obtener perfiles 2D y 3D de las implantaciones realizadas para tener un
mayor control de la operación y así dise~nar dispositivos más complejos. Debido a que los iones
implantados llevan trayectorias que podemos considerar aleatorias, existe una dispersión
lateral 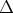 R
R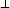 en las direcciones paralelas a la superficie del blanco (figura 3.12). Los
valores de
en las direcciones paralelas a la superficie del blanco (figura 3.12). Los
valores de 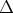 R
R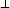 y
y 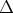 Rp son aproximadamente del mismo orden. Por lo tanto el área
implantada será mayor que la de la máscara. Este tipo de cuestiones actualmente tiene
mucha importancia debido a que las dimensiones de los dispositivos fabricados ha
decrecido considerablemente, tanto en las dimensiones paralelas a la superficie como en la
profundidad.
Rp son aproximadamente del mismo orden. Por lo tanto el área
implantada será mayor que la de la máscara. Este tipo de cuestiones actualmente tiene
mucha importancia debido a que las dimensiones de los dispositivos fabricados ha
decrecido considerablemente, tanto en las dimensiones paralelas a la superficie como en la
profundidad.
|
Una distribución bidimensional comúnmente empleada viene definida por la expresión:
![[ ( ) ( )]
n(x, y) = n(x)- erf c V~ y---a- - erf c V~ y-+-a-
2 2DR_ L 2DR_ L](tesis126x.gif) | (3.82) |
| La inspiración existe, pero |
| tiene que encontrarte trabajando |
| ~ Pablo Ruiz Picasso ~ |
Las condiciones del experimento deben estar bien definidas para obtener buenos resultados en la simulación. En este capítulo abordaremos este problema y a la vez describiremos las características de modelizado de la implantación que implementa el simulador, así como la mecánica básica de funcionamiento del mismo. En el capítulo siguiente desarrollaremos los puntos claves de naturaleza física de la simulación no descritos en éste.
Comenzaremos definiendo la estructura y propiedades del material blanco en la sección 4.2. La descripción de las condiciones de implantación modelizadas para el proyectil será tema de la sección 4.3. El funcionamiento básico del método Monte Carlo empleado en nuestro programa se considerará en la sección 4.4. La mejora estadística de los perfiles reduciendo a su vez el tiempo de cálculo será tema de la sección 4.5. La paralelización es otro mecanismo de reducción del tiempo de cálculo que se verá en la sección 4.6.
El simulador, está preparado para trabajar con cualquier material sólido multicapa1. Cada capa puede ser cristalina, policristalina o amorfa. El material objeto de la implantación no tiene que ser necesariamente un semiconductor.
Las capas se definen perpendiculares a un eje y son de extensión indefinida en los otros ejes. En la figura 4.1 se plantea un problema típico en el que aparece una capa de óxido nativo amorfo de un espesor dado, y el resto del material es silicio cristalino orientado según el eje cristalográfico {100} por ejemplo.
Cada capa de material se describe con un patrón regular, incluso si queremos una capa amorfa2. La celda patrón será repetida por el programa de forma periódica en todos los ejes.
Material cristalino: redes de Bravais. Existen 14 redes de cristalización diferentes, llamadas redes de Bravais (ver figura3 4.2), que se resumen en siete sistemas de cristalización distintos.
|
Nuestro programa permite definir la celda unidad de todas ellas a partir de 6 tipos diferentes de celdas básicas de posiciones de átomos paralelepipédicas cuyos ángulos y lados son definibles. (figura 4.3), que son:
Se definen asimismo sus ejes cristalográficos mediante tres ángulos (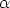 ,
, 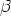 ,
, 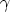 ) y tres distancias
(a, b, c) o parámetros de red. En la figura 4.2 se resumen las características de cada sistema de
cristalización.
) y tres distancias
(a, b, c) o parámetros de red. En la figura 4.2 se resumen las características de cada sistema de
cristalización.
El ejemplo más trivial en nuestras aplicaciones es la red de silicio que está compuesta por
dos subceldas cúbicas centradas en las caras (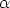 =
= 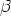 =
= 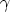 = 90), de las cuales una de ellas está
desplazada (0.25, 0.25, 0.25) unidades de red ( a = b = c = 5.431 Å) respecto de la otra.
En la figura 4.4 vemos la red de silicio descrita, en la que se observa claramente
el canal {110}, que es el más ancho de todos y objeto especial de estudio en este
trabajo.
= 90), de las cuales una de ellas está
desplazada (0.25, 0.25, 0.25) unidades de red ( a = b = c = 5.431 Å) respecto de la otra.
En la figura 4.4 vemos la red de silicio descrita, en la que se observa claramente
el canal {110}, que es el más ancho de todos y objeto especial de estudio en este
trabajo.
En la figura 4.5 puede observarse la estructura Zinc-Blenda del arseniuro de galio que comparte el sistema de cristalización del silicio pero con otros parámetros de red. Otras celdas más complejas pueden ser la del óxido de silicio (Fig. 4.6) que empleamos para definir la capa de óxido amorfo, o la del carburo de silicio [1, 73, 84] (SiC-6H) en la figura 4.7.
A pesar de que la definición del material se hace con el formato cristalino, nuestro programa permite tratar materiales amorfos y policristalinos.
Policristalino. Se simula el material policristalino suponiendo que para cada implantación completa de un átomo, todo el material es cristalino con la misma orientación. Antes de implantar un nuevo ion, se rota aleatoriamente el cristal de la capa en cuestión para obtener una nueva orientación. De esta manera intentamos reproducir las diferentes orientaciones cristalográficas presentes en un material policristalino. Este mecanismo es mejorable, pero para nuestras aplicaciones es razonablemente aceptable. Si quisieramos mejorar este modelo tendríamos que conocer el tama~no medio del grano del policristal, y una vez que el proyectil hubiese recorrido esa distancia, elegiríamos al azar una nueva orientación cristalográfica.
Amorfo. El material amorfo, se simula de una forma sencilla y muy parecida a la del material policristalino. Consiste en rotar el cristal después de cada colisión para generar un material amorfo que conserve la densidad. Este mecanismo da buenos resultados cuando lo comparamos con programas como TRIM que simula explícitamente implantaciones en materiales amorfos. Nuestro simulador no puede competir en velocidad con estos programas, sin embargo es una buena medida para comprobar la validez de nuestro programa con otros iones o con otros materiales.
Los átomos que componen cada capa del material están en continuo movimiento desplazandose de sus posiciones de equilibrio. Nuestra modelización del problema es sencilla. Consideramos que los átomos del cristal se encuentran desplazados de su posición de equilibrio una cantidad que responde al modelo de Debye, que depende de la temperatura del material. En nuestra simplificación consideramos que los átomos se encuentran en reposo en la posición que define el modelo de Debye. Su velocidad es despreciable en comparación con la velocidad del ion que colisiona con ellos [8].
El desplazamiento empleado es isotrópico y no está correlacionado [42]. Está distribuido a lo largo de cada coordenada ortogonal de acuerdo a una distribución gaussiana con una varianza dada por el modelo de Debye [11]. El desplazamiento será diferente para cada tipo de átomo. El modelo de Debye tiene como parámetro fundamental la temperatura de Debye (T Debye) del átomo en cuestión.
La amplitud RMS4 del desplazamiento térmico varía con la temperatura del material como sigue:
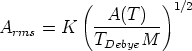 | (4.1) |
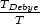 2 > 2.16 usaremos la expansión asintótica de la función de Debye5
2 > 2.16 usaremos la expansión asintótica de la función de Debye5
El problema fundamental al modelizar el material es conocer el valor de T Debye. Se han analizado multitud de experimentos y simulaciones para intentar conocer su valor, sin embargo, no hay unanimidad en los resultados. Para el silicio:
Nosotros empleamos, el valor de T Debye = 519 K para el silicio, que es un valor obtenido experimentalmente [18]. No utilizamos el valor de T Debye en nuestro modelo como parámetro ajustable como se hace a menudo en algunos modelos BCA [45]. Siempre usamos el mismo valor, únicamente dependiente de la naturaleza del átomo que vibra y no de las condiciones de implantación.
Al igual que con los átomos que componen el cristal, se define el ion que va a implantarse. Esto es, se define su símbolo, masa atómica, número atómico y temperatura de Debye6 asociada.
Ventana de implantación. El programa selecciona aleatoriamente el punto de llegada del proyectil dentro de la ventana de implantación según se aprecia en la figura 4.8. De esta forma podríamos obtener perfiles laterales ajustados a una máscara.
Divergencia del haz. Se define la divergencia del haz como el ángulo máximo de separación de un ion con respecto a la dirección nominal del proyectil. Utilizando este valor y un modelo estadístico obtendremos la dirección efectiva de incidencia de los distintos proyectiles implantados. Con esto se pretende reproducir el fenómeno de divergencia que aparece en los implantadores reales, que lógicamente no son capacez de proporcionar iones con una única dirección. Los modelos estadísticos que hemos implementado para la divergencia son los siguientes:
El simulador implementado se ha escrito completamente en C++. Empleamos la aproximación de colisiones binarias (BCA) que consiste en seguir la trayectoria del ion colisionando cada vez con un único átomo blanco. En cada colisión se evalúa una transferencia elástica de energía. Asociado al movimiento del ion existe una pérdida inelástica de energía, que también es tenida en cuenta. En esta sección estudiamos el funcionamiento del simulador desarrollado con la definición de una serie de procedimientos que son descritos a continuación.
Desarrollo de las cascadas. Inicialmente el proyectil principal se corresponde con el ion incidente. Sin embargo al desarrollarse la cascada de colisiones se pueden generar otros proyectiles secundarios, que generarán subcascadas a su vez (ver figura 4.10). Esto es interesante si se quiere hacer un estudio del da~nado generado, vacantes e intersticiales, etc. El seguimiento de los proyectiles secundarios no es cronológico, sino que sigue un criterio energético, siguiendo primero al que más energía tiene, hasta que se para. En ese momento, se escoge el ion secundario pendiente que más energía tenga. Existen estudios [86] que invitan a seguir cronológicamente las cascadas. Quizás tenga importancia cuando queramos simular el da~nado y su recombinación. Se suele prescindir del desarrollo completo de las cascadas cuando se calculan perfiles de impurezas, dado que estas no aportan ninguna información (no está implementado el da~nado) y se aumenta la velocidad de ejecución.
Condición de parada de un proyectil. Se considera que un proyectil se para cuando su energía está por debajo de una energía umbral ET (Threshold Energy) definida. Por defecto consideramos que vale ET = 10 eV con los proyectiles habituales.
Generación de proyectiles secundarios. Se generará un proyectil secundario cuando una colisión del proyectil primario con un átomo del blanco le transfiera una energía T que sea mayor que la energía de enlace, Eb, (Binding Energy) del átomo con la red. En realidad, representa el umbral de energía potencial que tiene que superar el átomo para salir de su pozo de potencial. Entonces el ion secundario se seguirá suponiendo que tiene una energía E = T - Eb.
Cambio de zona. La superación de una frontera entre dos capas, implica un tratamiento previamente definido. Cuando el ion se encuentra en la capa A y se aproxima a la capa B nuestro criterio es que siga viendo material tipo A hasta que su posición pertenezca al material B. Esto da una cierta histéresis en el comportamiento de las superficies entre los materiales, además de no considerar deformados o estresados los materiales en estos límites. Para nuestros propósitos, la aproximación es buena.
Búsqueda de blancos. El método de selección de los blancos se muestra en la figura 4.11. El
proyectil P se mueve con dirección 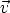 0. Los blancos con los que podría colisionar serían en
principio los que estén delante de él según la dirección de movimiento. Sin embargo, con átomos
como T 3 no debería colisionar, por que colisionó en la iteración anterior, y de esto se
asegura el programa comprobando que la distancia frontal de colisión sea mayor que
el valor de
0. Los blancos con los que podría colisionar serían en
principio los que estén delante de él según la dirección de movimiento. Sin embargo, con átomos
como T 3 no debería colisionar, por que colisionó en la iteración anterior, y de esto se
asegura el programa comprobando que la distancia frontal de colisión sea mayor que
el valor de  min, que por otra parte tiene un límite inferior distinto de cero que es
min, que por otra parte tiene un límite inferior distinto de cero que es
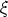 limite = 0.1 Å.
Se seleccionan entonces los átomos que estén dentro de un cilindro de radio, Rint, y altura
Dsim. Por lo tanto, no puede colisionar con T 4. Los únicos que cumplen las condiciones
impuestas en esta primera fase de selección son T 1 y T 2. Estos átomos podrían colisionar de
forma simultanea con el proyectil.
limite = 0.1 Å.
Se seleccionan entonces los átomos que estén dentro de un cilindro de radio, Rint, y altura
Dsim. Por lo tanto, no puede colisionar con T 4. Los únicos que cumplen las condiciones
impuestas en esta primera fase de selección son T 1 y T 2. Estos átomos podrían colisionar de
forma simultanea con el proyectil.
Se calculan de forma individual cada una de las colisiones binarias proyectil - blanco seleccionadas. En una segunda fase, se seleccionan aquellos átomos que, comenzando en la posición final (átomo en color negro) más cercana al proyectil no tenga su posición final más alejada que una cantidad Dsim2. Esto significa que ciertamente T 1 y T 2 colisionarán simultáneamente con el proyectil. Los valores típicos son Dsim = 1.0 Å, Dsim2 = 0.25 Å, y Rint = 2.7155 Å para el silicio. Estos valores dependerán del material blanco y no se utilizan como parámetros ajustables en cada simulación.
Corrección en la búsqueda de blancos. El procedimiento anterior, es el procedimiento estandar implementado en MARLOWE [88]. Sin embargo, hemos descubierto que en ciertas ocasiones el mecanismo es insuficiente y se colisiona con los mismos blancos más de una vez consecutiva. Esto es erroneo y modifica el perfil simulado de impurezas. Esto es debido a la presencia de las vibraciones térmicas que hacen que los átomos se desplacen aleatoriamente de sus posiciones de equilibrio, no siendo sencillo hacer la cuenta de todo para no recolisionar con los mismos átomos. Hemos corregido el problema manteniendo una lista de los últimos blancos con los que colisionamos. Si en la siguiente colisión aparecen repetidos, entonces los eliminamos de la lista de candidatos. Esta es una solución sencilla y efectiva. El número de átomos que mantenemos en la lista rara vez supera los tres blancos, por lo que no es muy costoso en tiempo de cálculo.
Colisiones simultaneas. Cuando el proyectil se encuentra con varios blancos con un parámetro de impacto similar y a una distancia frontal dentro de unos márgenes, se considera que todas las colisiones son importantes y es necesario tener en cuenta todos los átomos para describir mejor la colisión nuclear.
En la figura 4.12 se muestra el ejemplo típico de colisión simétrica en el que una resolución secuencial de las colisiones da unos resultados erróneos, ya que la dirección de salida se modifica con respecto a la incidente y no debe ser así. Utilizando el procedimiento de colisiones simultaneas se corrige este defecto, aunque la energía de salida del proyectil, se sobreestima.
El tratamiento de colisiones simultaneas consiste en resolver individualmente las
colisiones binarias del proyectil con los átomos seleccionados en el procedimiento
de búsqueda de blancos. Se obtendrán para cada átomo blanco una posición final,
una dirección de salida y una energía (ver figura 4.13). Así la colisión entre P y
T 1 nos dará una posición T 1' y una velocidad de salida 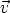 1 para el primer blanco.
Lo mismo ocurrirá entre P y T 2, dando una posición T 2' y una velocidad de salida
1 para el primer blanco.
Lo mismo ocurrirá entre P y T 2, dando una posición T 2' y una velocidad de salida
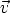 2.
2.
La composición de las colisiones binarias en una múltiple o simultanea está basada en la
aplicación de dos principios de conservación: el del momento y el de la energía. Al resolver estas
ecuaciones suponiendo que el estado final de los blancos es el descrito, se obtiene un estado final
P ' para el proyectil con una velocidad de salida 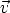 f . La posición final del proyectil
se escoge tomando el avance máximo obtenido para el proyectil en las colisiones
individuales.
f . La posición final del proyectil
se escoge tomando el avance máximo obtenido para el proyectil en las colisiones
individuales.
Finalmente se calculará el valor de 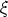 min para que en la siguiente iteración no se vuelva a
colisionar con los mismos blancos.
min para que en la siguiente iteración no se vuelva a
colisionar con los mismos blancos.
Para la correcta caracterización de los perfiles de impurezas, es necesario obtener una determinada precisión estadística en las zonas de menor concentración de los mismos. Esto es interesante sobre todo en las implantaciones con acanalamiento, en las que la zona acanalada del perfil puede estar varios órdenes de magnitud por debajo del máximo de concentración. Unido a esto, está la imperiosa necesidad de reducir el tiempo de computación a unos niveles mínimos, para lo cual es muy útil un algoritmo de mejora de sucesos poco probables o de rare event.
Una vez estudiados los diferentes modelos propuestos por otros autores (ver sección 3.3) y vistas sus ventajas e inconvenientes, decidimos implementar un modelo propio mejorando los anteriores en algunos aspectos. Hemos partido del modelo de Beardmore [8] y realizamos un estudio metodológico que describimos a continuación de lo que queríamos mejorar.
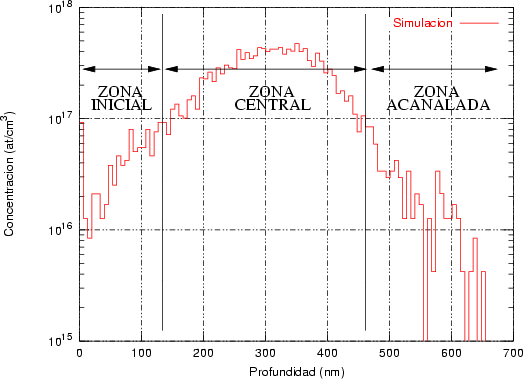
|
El algoritmo comprueba si el proyectil ha superado ciertas fronteras Di, (1 < i < N), o bien en profundidad, o bien en distancia recorrida. Estas fronteras se calculan de forma dinámica (ver sección 3.3 en la página 120) cumpliendo que
![integral integral
di 1-i oo
0 C(x)dx = [1- (2) ] 0 C(x)dx](tesis164x.gif) | (4.2) |
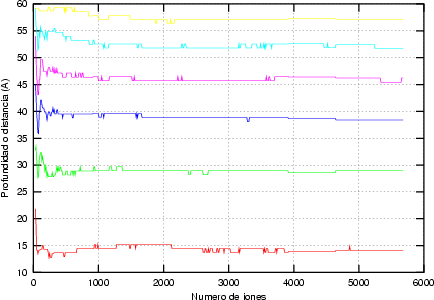
|
Si el proyectil que inicialmente tiene peso estadístico unidad (w = 1) supera una de esa fronteras, entonces se divide en n iones virtuales cada uno con un peso estadístico (ver figura 4.16):
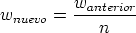 | (4.3) |
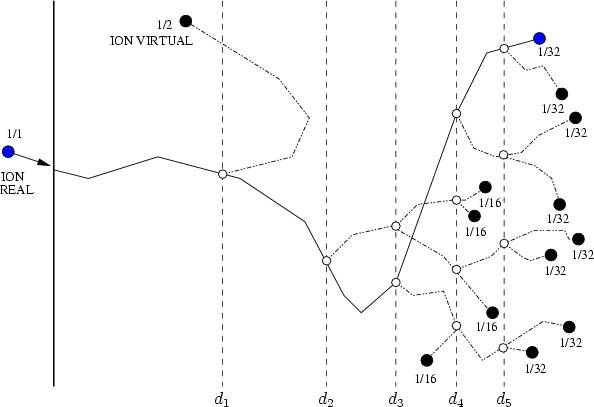
|
El resultado del algoritmo se puede apreciar en la figura 4.17 donde se comparan dos simulaciones con el mismo número de iones reales (Niones = 2000) y en la que el algoritmo de rare event ha sido programado para dar dos órdenes de magnitud más de exactitud (M = 2).
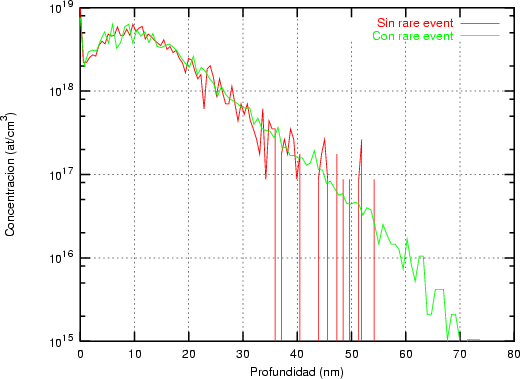
|
El algoritmo básico se basa en la profundidad que ha alcanzado el ion dentro del material. Si deseamos representar un perfil bidimensional, lograremos mejorar la estadística de las zonas más profundas (ver figura 4.18 (a) y (b)).
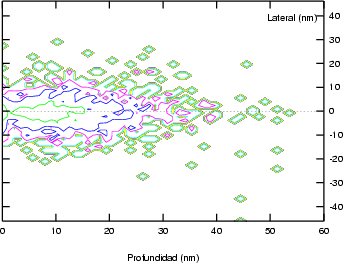 (a) Sin rare event . 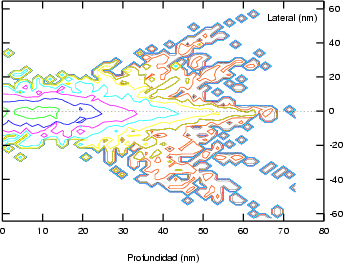 (b) Con rare event en profundidad. 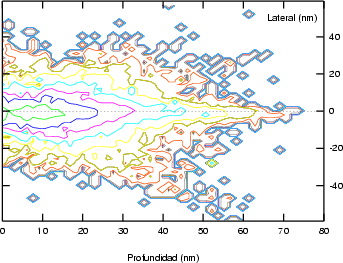 (c) Con rare event en distancia.
|
Sin embargo, parece muy interesante en las aplicaciones microelectrónicas actuales conocer no sólo la distribución de impurezas en profundidad, sino conocer la dispersión lateral de los perfiles que en un caso general no responderán a ninguna fórmula particular. En este caso, en el que queremos mejorar la precisión estadística de las distribuciones laterales, lo que hacemos es implementar el algoritmo de rare event basándonos en la distancia recorrida por el ion en cuestión (ver figura 4.18 (c)). Se contabiliza para cada ion la longitud recorrida para así determinar cuales han recorrido más distancia. El mecanismo utilizado es el descrito, solo que empleando distancias recorridas en lugar de profundidades alcanzadas.
|
En la tabla 4.19 se muestra una comparativa de tiempos e iones virtuales simulados que se corresponden con las figuras mostradas anteriormente. Se observa que con un aumento de tiempo no muy significativo se consigue mejorar el perfil en dos órdenes de magnitud, mientras que sin el algoritmo de rare event una mejora de un orden de magnitud (Niones = 20000) aumenta mucho el tiempo de cálculo.
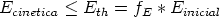 | (4.4) |
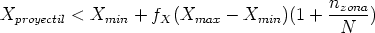 | (4.5) |
Los factores fE y fX se definen por fichero de entrada y valen por defecto fE = 0.30 y fX = 0.30. En la figura 4.21 se muestra el resultado de aplicar el rare event en superficie. El tiempo de cálculo se incrementa en un 7 %, pero se mejora la estadística en superficie.
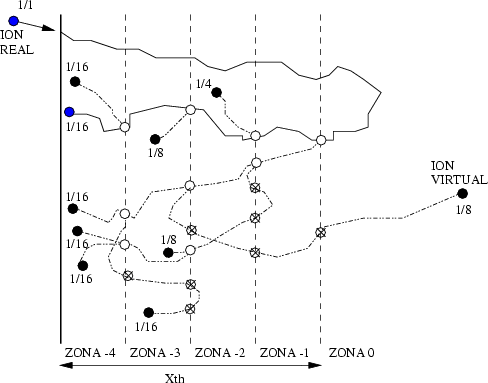
|
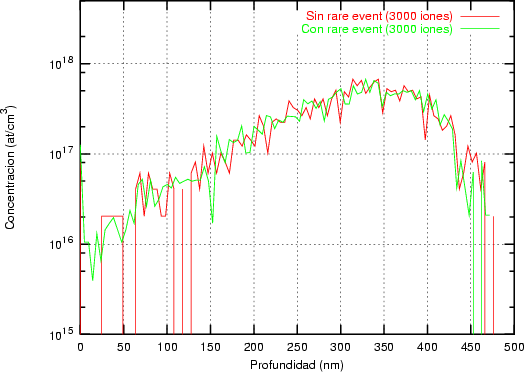
|
El algoritmo comienza a funcionar cuando se ha implantado un número determinado de iones reales REThreshold para evitarnos así el conocer a priori7 la forma del perfil en cuestión y que sea el própio programa el que defina las distancias o profundidades de subdivisión. Será necesario que este valor sea lo suficientemente grande (valor típico = 100) como para tener algo de estadística.
Después se actualizan dinámicamente las profundidades o distancias de subdivisión cuando se han implantado un número REInterval de iones más. Tiene que ser un valor no demasiado peque~no (p. ej. 100) para no penalizar el funcionamiento del programa. Así se consigue optimizar el funcionamiento del algoritmo para proyectiles acanalados.
El número de veces que se subdivide una trayectoria está limitado por la precisión definida, M, de manera que el número máximo coincide con el mayor entero < M log 2(10). Este valor se emplea también en el rare event en superficie. Así si N = 6, un ion real podría descomponerse hasta en 26 = 64 iones virtuales.
Cuando se llevan implantados un número grande de iones reales, se supone que hemos alcanzado de sobra la precisión estadística que deseabamos en las zonas de interés por lo que el algoritmo se desactiva, para que el esfuerzo computacional se centre en la zona de los máximos del perfil.
Uno de los requisitos, es que el simulador sea rápido. En el desarrollo y dise~no de nuevos dispositivos microelectrónicos no es permisible que una simulación de uno de los numerosos procesos de los que se compone la fabricación del circuito integrado, lleve tiempos del orden de horas o incluso de varios días.
Dado que la potencia computacional de pico está limitada por el hardware utilizado, una buena forma de conseguir aumentar la potencia de cálculo mantenida es el uso del paralelismo intensivo. Cuanto mayor sea el número de máquinas empleadas en la resolución de un problema, mayor será la potencia de cálculo disponible. El crecimiento no es del todo lineal (ver figura 4.22) con el número de máquinas ya que las comunicaciones entre ellas llevan tiempo y suelen ser el cuello de botella de toda máquina paralela.
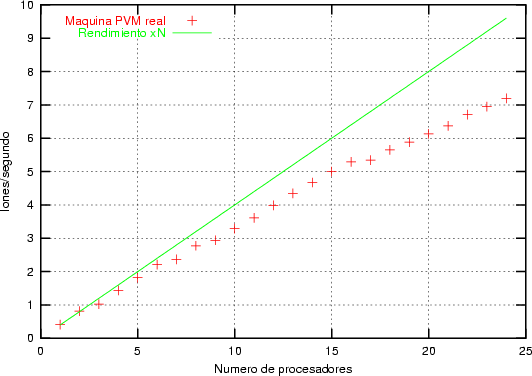
|
Disponer de una máquina paralela actualmente está en la mano de cualquier centro de investigación y/o desarrollo, ya que su precio se ha reducido en los últimos a~nos. Pero, el paralelismo se ve limitado por el número de procesadores que incorpore dicha máquina. La solución está en interconectar varias de esas máquinas, paralelas o no, para aumentar el número de procesadores total.
Sin embargo, y por lo general, se dispone de máquinas de diversos tipos, con código no compatible y de dificil intercomunicación, que no son aprovechadas. Nosotros hemos optado por una solución que incorpore todo tipo de máquinas disponibles, incluyendo las obsoletas, ya que aunque su potencia de cálculo sea inferior a la de las máquinas actuales el trabajo en equipo hace que todo vaya más rápido. Hay que rentabilizar las inversiones de hace a~nos. La interconexión de las máquinas se hace a través del protocolo TCP/IP, que es el estándar en Internet.
Hemos implementado una versión paralela utilizando una biblioteca de dominio público denominada Parallel Virtual Machine (PVM) [76, 28, 97] que permite trabajar en una máquina virtual con un número variable de máquinas, monoprocesador o multiprocesador, heterogéneas. Esto implica que máquinas diferentes pueden trabajar en común para resolver el mismo problema. Lo único necesario es que el código fuente del programa se compile por separado en cada máquina.
El grado de paralelismo obtenido es de grano gordo. Esto se llama así por que cada procesador hace una tarea muy compleja sin interactuar apenas con los demás. Esto es posible en nuestro programa dado que nuestra tarea es implantar iones. El seguimiento completo de una cascada es para nosotros la tarea compleja, que va a ser ejecutada en cada procesador de cada máquina. La intercomunicación entre los diferentes procesos servirá para que no trabajen de forma independiente si no que los resultados de un proceso influyan en los de las demás.
Dado que no está implementado un modelo de da~nado, que sin duda complicaría notablemente el tratamiento propuesto, es relativamente sencillo implementar una versión en paralelo de nuestro programa . En la figura 4.23 se muestra el esquema maestro-esclavo seguido en la implementación paralela del simulador.
| La Virgen se aparece a los pastores... |
| porque los pastores están en el campo |
| ~ Dicho popular ~ |
En el desarrollo de la simulación de la implantación iónica se considera que el ion incidente colisiona tan solo con un átomo blanco cada vez. Esto es lo que se llama aproximación de colisiones binarias o BCA1. Este punto es el que distingue nuestro trabajo de otros similares basados en Dinámica Molecular, en los cuales se contempla la resolución del problema desde un punto de vista más preciso. Sin embargo el método BCA proporciona resultados aceptables en un tiempo considerablemente menor. Para mejorar aquellos casos en los que la secuencialización de las colisiones individuales con varios átomos no sea posible, hemos desarrollado un mecanismo de colisiones simultaneas, que mejorará la aproximación BCA (Ver la sección 4.4 del capítulo anterior).
La transferencia de energía entre dos partículas puntuales cargadas depende clásica-mente de la masa, de la distribución de carga y de la velocidad y posiciones iniciales de ambas partículas. Usaremos una resolución asintótica de las trayectorias de las partículas suponiendo que el proyectil viene del infinito y después de la colisión se aleja hasta el infinito. Necesitaremos además una descripción precisa de la distribución electrónica para el cálculo de los potenciales interatómicos entre las partículas que intervienen en el problema.
El cálculo de las pérdidas inelásticas de energía es muy importante para la correcta simulación de la implantación iónica, sobre todo en situaciones de acanalamiento. Nosotros hemos mejorado los modelos de frenado existentes para conseguir que no dependan de parámetros ajustables, con la excepción de rs0 que depende del ion Z1 que se implanta y que sirve de mecanismo para reproducir las llamadas oscilaciones Z1 [31, 69].
En la sección 5.2.1 resolveremos analíticamente el problema de la colisión de dos partículas cargadas y en la sección 5.2.2 propondremos una solución numérica rápida al mismo problema. En la sección 5.2.3 veremos como hemos calculado los potenciales interatómicos específicos que empleamos en el cálculo del frenado nuclear a partir de distribuciones electrónicas de estado sólido [118] y de átomos aislados [91]. El problema del frenado inelástico se trata en las secciones siguientes, viendo cuales han sido las soluciones que hemos implementado tanto para el frenado electrónico (sección 5.3.1) como para el inelástico própiamente dicho (sección 5.3.2).
Podemos abordar el problema de las colisiones binarias como la resolución clásica del choque entre dos partículas cargadas en el que se conserva la energía y el momento. Con las energías y masas empleadas los efectos relativistas no son importantes. Suponemos (ver figura 5.1) que el proyectil de número atómico Z1, y masa M1 avanza con una energía EP y el átomo blanco de número atómico Z2 y masa M2 está en reposo2.
Las ecuaciones de movimiento de las dos partículas serán:
donde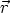 1 es la posición del proyectil y
1 es la posición del proyectil y 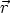 2 la del blanco y
2 la del blanco y 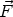 es la fuerza central que actúa sobre
las partículas y que vale:
es la fuerza central que actúa sobre
las partículas y que vale:
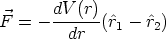 | (5.2) |
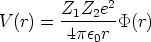 | (5.3) |
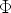 (r), se puede tomar como específica de los átomos que
intervienen (ver cálculo detallado en la sección 5.2.3) o como universal [118] obtenida a través
de un ajuste de potenciales interatómicos específicos que son reescalados via una distancia de
apantallamiento universal:
(r), se puede tomar como específica de los átomos que
intervienen (ver cálculo detallado en la sección 5.2.3) o como universal [118] obtenida a través
de un ajuste de potenciales interatómicos específicos que son reescalados via una distancia de
apantallamiento universal:
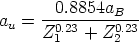 | (5.4) |
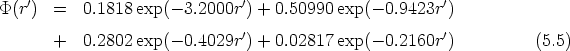
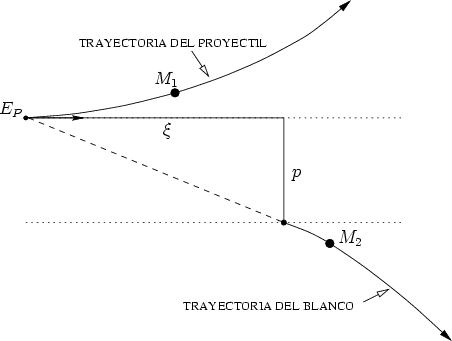
|
Los ángulos formados por las asíntotas de salida y la dirección incidente son [66]:
![integral oo [ 2 ]-1
Q = p - 2p R dr r g(r) (5.6)
P = Q - p](tesis188x.gif)
![[ p2 (1 + A)V (r)]1/2
g(r) = 1- -2-- ------------
r AEcm](tesis189x.gif) | (5.7) |
La integral de tiempo, que es la diferencia entre el tiempo que emplearía una partícula libre
de interacciones en alcanzar la posición ápside y el que realmente emplea el proyectil,
multiplicado por la velocidad inicial del proyectil, da una distancia  (ver figura 5.3):
(ver figura 5.3):
![integral oo [ 2 ]
t = (R2 - p2)1/2- dr -1--- (1- p-)-1/2
R g(r) r2](tesis190x.gif) | (5.8) |
 ,
, 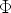 ) y el sistema de referencia del
laboratorio (
) y el sistema de referencia del
laboratorio (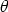 ,
, 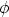 ):
): 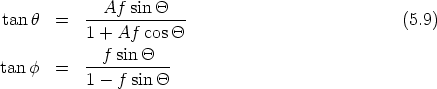
![[ M Q ] 1
x1 = (1 + f )t + (f--2- - 1)- ptan -- ---------------
M 1 2 f(1 + M2/M1)
Q
x2 = ptan 2-- x1](tesis192x.gif)
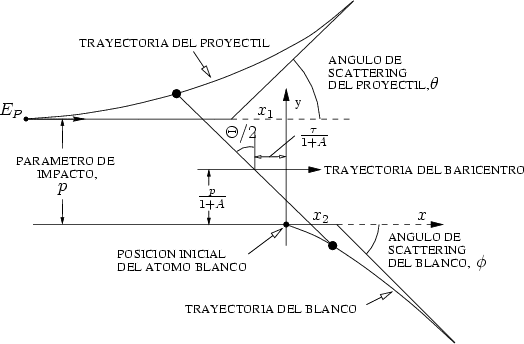
|
Las direcciones de salida de ambas trayectorias en el sistema de referencia laboratorio valdrán
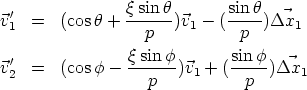
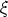 es la distancia de colisión frontal (figura 5.1).
es la distancia de colisión frontal (figura 5.1).
El factor de corrección f empleado en la aproximación cuasielástica se define como:
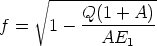 | (5.10) |
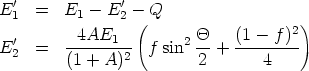
Nosotros no contabilizamos el frenado inelástico a través de Q, sino que seguimos un procedimiento más exacto descrito en la sección 5.3 en el que las pérdidas son integradas a lo largo de la trayectoria de tramos rectos que sigue el proyectil.
La resolución analítica es costosa computacionalmente hablando. Se ha de calcular el ápside de la trayectoria resolviendo una ecuación trascendental (g(R) = 0), para lo que se emplea un algoritmo Newton-Raphson iterativo. Las integrales que aparecen se resuelven empleando una aproximación numérica mediante integrales de Mehler. Por lo tanto, es muy interesante buscar una alternativa más rápida.
Las tablas son generadas automáticamente por nuestro programa para cada pareja de átomos Z1, Z2 que intervienen en la simulación, si no son localizadas en el disco.
En la figura 5.4 vemos el esquema de salida. En realidad, tan solo se almacenan los valores
de x1, x2, E1, E2 y cos(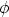 ). Para finalizar la resolución se aplican los teoremas de conservación
del momento y de la energía, incluyendo las pérdidas inelásticas que se verán en la sección 5.3.
Por eso, el valor de
). Para finalizar la resolución se aplican los teoremas de conservación
del momento y de la energía, incluyendo las pérdidas inelásticas que se verán en la sección 5.3.
Por eso, el valor de 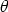 no es necesario ya que se obtiene al aplicar el teorema de conservación del
momento a la colisión.
no es necesario ya que se obtiene al aplicar el teorema de conservación del
momento a la colisión.
|
Los parámetros de entrada necesarios en nuestra resolución asintótica del problema de la colisión binaria se muestran en la figura 5.5, en la que se indica el rango cubierto y el número de puntos precalculados. Los rangos no son cubiertos con un espaciado lineal, si no cumpliendo unas determinadas leyes logaritmicas.
El tama~no de nuestras tablas es de
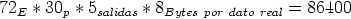 |
El uso de un potencial interatómico universal simplifica en buena medida el desarrollo de las simulaciones ya que no se necesita más información de los átomos que su masa y su número atómico. Sin embargo un potencial interatómico especificamente calculado para una pareja de átomos dará mayor exactitud al problema y por consiguiente mejorará los resultados.
En principio, y para simplificar el problema vamos a utilizar tan solo potenciales interatómicos repulsivos que vendrán definidos como un potencial culombiano apantallado. La función de apantallamiento, será pues, el punto importante a desarrollar. En los siguientes puntos revisaremos los potenciales universales más comúnmente empleados y abordaremos el problema de un cálculo aproximado de potenciales repulsivos específicos.
Los potenciales repulsivos universales se describen como un potencial culombiano apantallado, es decir,
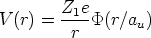 |
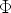 (r/au) es una función de apantallamiento universal
que depende de la distancia normalizada, siendo au:
(r/au) es una función de apantallamiento universal
que depende de la distancia normalizada, siendo au:
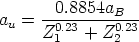 |
Las funciones de apantallamiento, 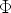 , universales típicas, aparecen en la figura 5.6. Hemos
empleado en todas ellas la longitud de apantallamiento au.
, universales típicas, aparecen en la figura 5.6. Hemos
empleado en todas ellas la longitud de apantallamiento au.
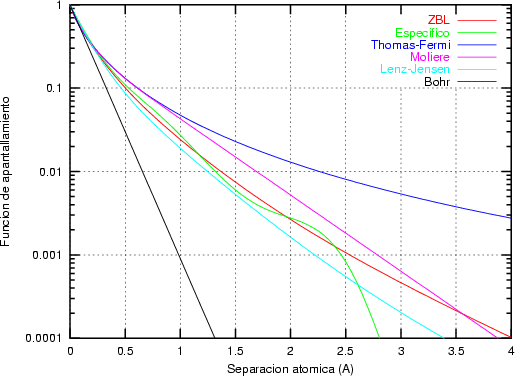
|
Revisamos algunas funciones de apantallamiento universales a modo de resumen, que fueron calculados por sus respectivos autores modelizando los átomos y sus densidades de carga. Se corresponden con un ajuste para muchas parejas de átomos, que está escalado a través del factor au:
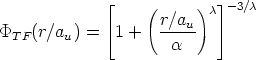 |
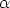 = 122/3 y
= 122/3 y 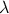 = 0.8034.
= 0.8034.
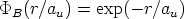 |
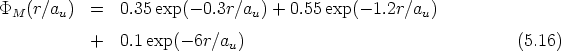
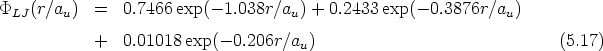
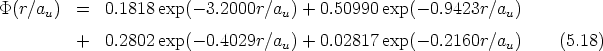
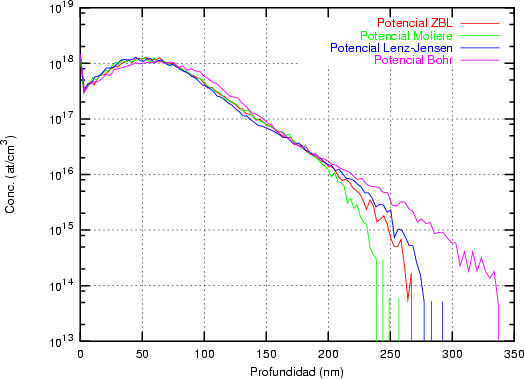
|
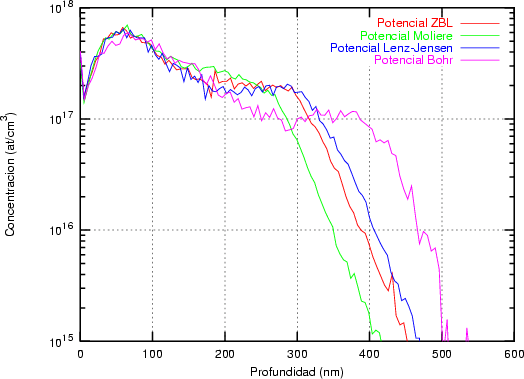
|
En la figura 5.7 podemos observar las diferencias que se obtienen en un perfil para
direcciones de bajo acanalamiento cuando se emplean diferentes potenciales universales para
implantaciones en el canal {100} con ( ,
,  ) = (7, 30) grados. Sólamente se observan diferencias
en la cola del perfil.
) = (7, 30) grados. Sólamente se observan diferencias
en la cola del perfil.
Si realizamos la comparación para la simulación de una implantación en el canal {110} (ver figura 5.8) vemos que las diferencias son mayores, y que afectan fundamentalmente al pico de acanalamiento.
El potencial universal es un ajuste realizado sobre un gran conjunto de potenciales específicos. Por ello en algunos casos este no describirá el problema con toda la exactitud que queremos. En un intento de eliminar aproximaciones calculamos un potencial interatómico específico por cada par de átomos que intervienen en la simulación.
Para cada átomo se supone una distribución de carga esférica, 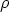 (r), con una carga puntual
Zie en el centro de forma que se cumple que Zie =
(r), con una carga puntual
Zie en el centro de forma que se cumple que Zie = 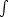
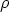 idx3. Suponemos que el átomo está en un
sólido y que sus electrones están confinados en una celda limitada espacialmente [118]. En el
caso de los átomos del material empleamos distribuciones de densidad radiales del tipo
Hartree-Fock de estado sólido. Para los iones usamos distribuciones radiales de átomos aislados
calculadas con el programa GAMESS [91]. En la figura 5.9 podemos comparar las diferencias
entre ambos tipos de distribuciones.
idx3. Suponemos que el átomo está en un
sólido y que sus electrones están confinados en una celda limitada espacialmente [118]. En el
caso de los átomos del material empleamos distribuciones de densidad radiales del tipo
Hartree-Fock de estado sólido. Para los iones usamos distribuciones radiales de átomos aislados
calculadas con el programa GAMESS [91]. En la figura 5.9 podemos comparar las diferencias
entre ambos tipos de distribuciones.
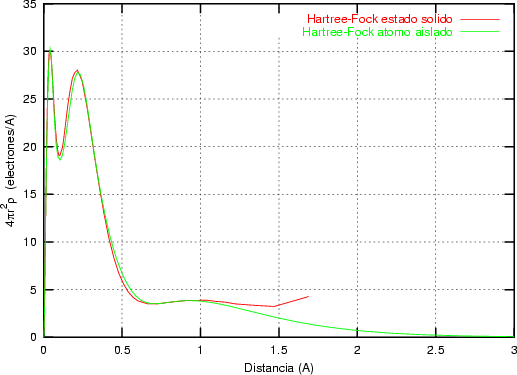
|
Cuando el ion comienza a interaccionar con el átomo suponemos que no hay distorsión espacial de las distribuciones electrónicas, y que el núcleo permanece en el centro de dicha distribución. La energía potencial de interacción valdrá:
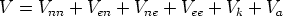 | (5.19) |
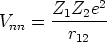 | (5.20) |
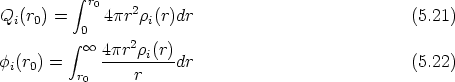
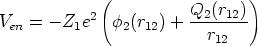 | (5.23) |
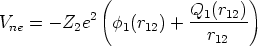 | (5.24) |
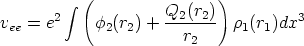 | (5.25) |
Para V k y V a consideraremos que en la zona de solapamiento de las distribuciones electrónicas la energía debe cambiar de acuerdo con el principio de Pauli. Tratando este volumen como un gas de electrones libres completamente degenerado y suponiendo que no existen distorsiones en ambas cargas, el exceso de energía cinética valdrá [118]:
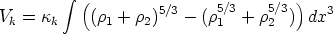 | (5.26) |
 k = 21.88 eV Å.
La energía de intercambio, se entiende comprendiendo que en la vecindad de cada electrón
la densidad de electrones con la misma dirección de spin es sustancialmente menor que en el
caso de una distribución uniforme. La energia de intercambio total de las distribuciones
electrónicas solapadas es:
k = 21.88 eV Å.
La energía de intercambio, se entiende comprendiendo que en la vecindad de cada electrón
la densidad de electrones con la misma dirección de spin es sustancialmente menor que en el
caso de una distribución uniforme. La energia de intercambio total de las distribuciones
electrónicas solapadas es:
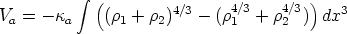 | (5.27) |
 a = 10.635 eV Å.
La función de apantallamiento se definirá entonces como:
a = 10.635 eV Å.
La función de apantallamiento se definirá entonces como:
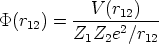 | (5.28) |
En la figura 5.11 se representa el potencial específico calculado para la pareja B - Si. Se aprecian algunas diferencias notables entre el potencial específico y el universal ZBL, sin embargo, las diferencias entre los perfiles calculados con el potencial específico y el potencial universal ZBL, en este caso, no son significativas como se aprecia en la figura 5.12, debido a que para los iones ligeros es más importante la pérdida energética debida al frenado inelástico que la debida a las colisiones nucleares.
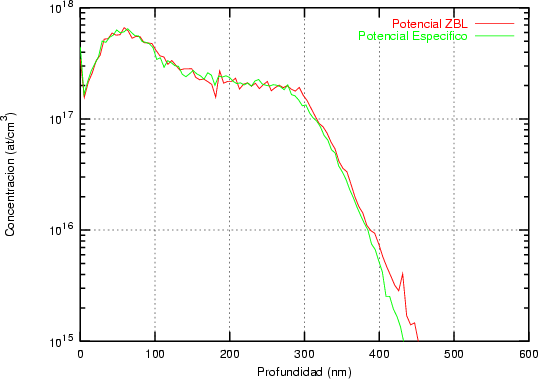
|
Una vez se han calculado las posiciones y velocidades de salida del proyectil y de los blancos en una colisión meramente nuclear, se procede al cálculo del frenado inelástico asociado a ella. Estamos suponiendo que el frenado nuclear y el frenado inelástico se pueden separar. Hacemos esta aproximación para que el problema pueda ser resuelto con rapidez, ya que no es factible ir integrando ambas pérdidas a lo largo de la trayectoria dentro del esquema BCA5.
Las pérdidas inelásticas de energía tienen dos componentes:
El modelo físico empleado para el frenado electrónico se estudia en la sección 5.3.1, mientras que el modelo de frenado inelástico se trata en la sección 5.3.2. La integración de las pérdidas inelásticas a lo largo de la trayectoria del proyectil tiene una planificación especial que se ve en la seccion 5.3.3.
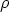 (x), o de forma equivalente del radio de un electrón rs = [3/(4
(x), o de forma equivalente del radio de un electrón rs = [3/(4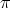
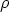 (x))]1/3; el
otro es el frenado electrónico del protón, Sp(v, rs). Dentro de la aproximación de densidad local
(LDA: local density approximation), la perdida inelástica de energía
(x))]1/3; el
otro es el frenado electrónico del protón, Sp(v, rs). Dentro de la aproximación de densidad local
(LDA: local density approximation), la perdida inelástica de energía 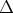 Ee de un ion a velocidad
constante v es
Ee de un ion a velocidad
constante v es
![integral
* 2
DEe = [Z 1(v,rs)]Sp(v,rs)dx](tesis222x.gif) | (5.29) |
![integral
DE = [Z*(v,ro)]2 S (v,r )dx
e 1 s p s](tesis223x.gif) | (5.30) |
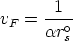 | (5.31) |
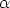 = [4/(9
= [4/(9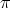 )]1/3. El valor rso es el único parámetro ajustable de este modelo de frenado
electrónico.
Tomamos un modelo estadístico simple para este proyectil móvil, parcialmente ionizado.
Para un ion con N = Z1 - Q electrones ligados, donde Q es la carga del ion de número átomico
Z1, una densidad de carga radialmente simétrica como
)]1/3. El valor rso es el único parámetro ajustable de este modelo de frenado
electrónico.
Tomamos un modelo estadístico simple para este proyectil móvil, parcialmente ionizado.
Para un ion con N = Z1 - Q electrones ligados, donde Q es la carga del ion de número átomico
Z1, una densidad de carga radialmente simétrica como
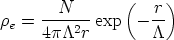 | (5.32) |
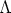 es el parámetro del tama~no del ion, función de la fracción de
ionización q = (Z1 - N)/Z1. La energía total de los electrones se obtiene de la suma de las
energías cinéticas estimadas por la aproximación de densidad local, la interación
electrón-electrón en la aproximación de Hartree, ponderada con un parámetro variacional
es el parámetro del tama~no del ion, función de la fracción de
ionización q = (Z1 - N)/Z1. La energía total de los electrones se obtiene de la suma de las
energías cinéticas estimadas por la aproximación de densidad local, la interación
electrón-electrón en la aproximación de Hartree, ponderada con un parámetro variacional 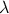 para tener en cuenta la correlación, y la energía de Coulomb de los electrones en el campo
eléctrico de los núcleos. Una aproximación variacional minimizando la energía total nos
conduce a la siguiente dependencia del tama~no del ion en la fracción de ionización q:
para tener en cuenta la correlación, y la energía de Coulomb de los electrones en el campo
eléctrico de los núcleos. Una aproximación variacional minimizando la energía total nos
conduce a la siguiente dependencia del tama~no del ion en la fracción de ionización q:
![2/3
/\ = ---2a0(1---q)------
Z1/13 [1- (1 - q)/7]](tesis226x.gif) | (5.33) |
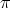
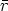 s3). El frenado electrónico total se estima como la suma de las pérdidas débiles de
energía de las colisiones distantes p.ej., peque~nas transferencias de momento con los electrones
del blanco que ven una carga qZ1, y la pérdida energética de los electrones del blanco que
experimentan un incremento de las interaciones nucleares en las colisiones cercanas que se
corresponden con grandes transferencias de momento. Tal y como se discute extensamente en la
literatura [17, 57, 118], se supone que el estado de carga de un protón es la unidad. Dada
una fracción de ionización q y utilizando como argumento de escalado el cociente
entre el frenado del ion y el frenado del protón a la misma velocidad, la teoría de
BK proporciona una expresión sencilla para la fracción de carga efectiva de un ion
s3). El frenado electrónico total se estima como la suma de las pérdidas débiles de
energía de las colisiones distantes p.ej., peque~nas transferencias de momento con los electrones
del blanco que ven una carga qZ1, y la pérdida energética de los electrones del blanco que
experimentan un incremento de las interaciones nucleares en las colisiones cercanas que se
corresponden con grandes transferencias de momento. Tal y como se discute extensamente en la
literatura [17, 57, 118], se supone que el estado de carga de un protón es la unidad. Dada
una fracción de ionización q y utilizando como argumento de escalado el cociente
entre el frenado del ion y el frenado del protón a la misma velocidad, la teoría de
BK proporciona una expresión sencilla para la fracción de carga efectiva de un ion
![[ ]
(4/\)2
g(v,rs) = q(v) + C(rs)(1 - q(v)) ln 1 + ---
rs](tesis228x.gif) | (5.34) |
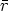 s) depende ligeramente del blanco y tiene un valor próximo a 1/2. Usaremos C = 0.5.
Entonces, la carga efectiva es
s) depende ligeramente del blanco y tiene un valor próximo a 1/2. Usaremos C = 0.5.
Entonces, la carga efectiva es
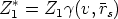 | (5.35) |
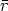 s se
identifica con la dependencia del valor medio rso. Por consiguiente, la carga efectiva Z1* tiene
un carácter no local (espacialmente), y depende de la superficie de Fermi. En la anterior
discusión, como hemos podido ver, q es un parámetro que no está fijado en la teoría de BK.
Para obtener esta fracción de la ionización existen criterios de velocidad y energía originalmente
propuestos por Bohr [13, 14] y Lamb [58] respectivamente. Kitagawa también usa un
argumento estadístico para justificar el escalado en terminos del parámetro de escalado
v1/(vBZ12/3).
Recientemente, se ha estudiado qué criterio tiene una mejor comprensión física [69].
Sin embargo, a la luz de la gran cantidad de datos experimentales empleados en
la Ref. [118] para extraer un escalado de la ionización consistente con la teoría de
Brandt-Kitagawa, utilizaremos este escalado verificado experimentalmente en este
modelo. Tal y como se resume en la Ref. [118] se propone un nuevo criterio en la
teoría de BK: un criterio de velocidad relativa [57], que supone que los electrones
del ion que tienen una velocidad orbital menor que la velocidad relativa entre el
ion y los electrones en el medio son eliminados. La velocidad relativa vr se obtiene
hallando la media sobre la diferencia entre la velocidad del ion v1 y la velocidad de los
electrones ve bajo la suposición de que los electrones de conducción están en un gas de
electrones libres. Realizando una nueva media de ve sobre la esfera de Fermi llegamos a
s se
identifica con la dependencia del valor medio rso. Por consiguiente, la carga efectiva Z1* tiene
un carácter no local (espacialmente), y depende de la superficie de Fermi. En la anterior
discusión, como hemos podido ver, q es un parámetro que no está fijado en la teoría de BK.
Para obtener esta fracción de la ionización existen criterios de velocidad y energía originalmente
propuestos por Bohr [13, 14] y Lamb [58] respectivamente. Kitagawa también usa un
argumento estadístico para justificar el escalado en terminos del parámetro de escalado
v1/(vBZ12/3).
Recientemente, se ha estudiado qué criterio tiene una mejor comprensión física [69].
Sin embargo, a la luz de la gran cantidad de datos experimentales empleados en
la Ref. [118] para extraer un escalado de la ionización consistente con la teoría de
Brandt-Kitagawa, utilizaremos este escalado verificado experimentalmente en este
modelo. Tal y como se resume en la Ref. [118] se propone un nuevo criterio en la
teoría de BK: un criterio de velocidad relativa [57], que supone que los electrones
del ion que tienen una velocidad orbital menor que la velocidad relativa entre el
ion y los electrones en el medio son eliminados. La velocidad relativa vr se obtiene
hallando la media sobre la diferencia entre la velocidad del ion v1 y la velocidad de los
electrones ve bajo la suposición de que los electrones de conducción están en un gas de
electrones libres. Realizando una nueva media de ve sobre la esfera de Fermi llegamos a

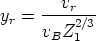 | (5.38) |
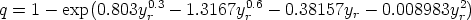 | (5.39) |
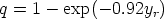 | (5.40) |
![( ) [ ( ) ]
dE- = 2v- ln 1 + -p-- - ----1-----
dx R 3p ars 1 + ars/p](tesis237x.gif) | (5.41) |
 -2
dE- = 2v- ln 1 + -2--- - 3pvF----1 1 - --1--
dx LW 3p 3pvF 3pvF + 2 3pvF](tesis238x.gif) | (5.42) |
![oo
dE-= -3v-- sum (l + 1) sin2 [d (E )- d (E )]
dx kF r3sl=0 l F l+1 F](tesis239x.gif) | (5.43) |
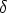 l(EF ) es el desplazamiento de fase en la energía de Fermi para la dispersión de un
electrón de momento angular l (kF es el momento de Fermi). En las Ref. [118, 65] la
comparación con los datos experimentales demuestra que el tratamiento de la densidad
funcional mejora el resultado de la respuesta (dielectrica) lineal, que subestima el frenado. El
frenado para el protón dentro de la teoría no lineal lo podemos expresar como [2]:
l(EF ) es el desplazamiento de fase en la energía de Fermi para la dispersión de un
electrón de momento angular l (kF es el momento de Fermi). En las Ref. [118, 65] la
comparación con los datos experimentales demuestra que el tratamiento de la densidad
funcional mejora el resultado de la respuesta (dielectrica) lineal, que subestima el frenado. El
frenado para el protón dentro de la teoría no lineal lo podemos expresar como [2]:
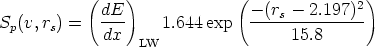 | (5.44) |
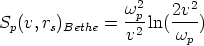 | (5.45) |
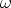 p =
p = 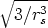 es la frecuencia de plasma electrónica.
El modo de seleccionar un modelo u otro es simple. Se toma el valor del modelo de
Echenique hasta donde se produce el segundo corte (no se muestra en la figura 5.14) con la
curva de Bethe, y después se toma el modelo de Bethe.
es la frecuencia de plasma electrónica.
El modo de seleccionar un modelo u otro es simple. Se toma el valor del modelo de
Echenique hasta donde se produce el segundo corte (no se muestra en la figura 5.14) con la
curva de Bethe, y después se toma el modelo de Bethe. 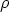 (x)
para los átomos del material en el cristal. Hemos empleado tres representaciones de la
distribución de carga:
(x)
para los átomos del material en el cristal. Hemos empleado tres representaciones de la
distribución de carga:
 (a) Densidad ZBL 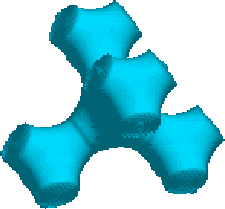 (b) Densidad con enlaces completos  (c) Densidad ISDS (superposición de densidades de átomos aislados)
|
Densidad electrónica radial. En el caso de átomos de silicio, utilizamos una distribución de carga atómica Hartree-Fock de estado sólido, que es simétrica y esférica debido a su construcción muffin tin. Con esta aproximación tenemos cerca de un electrón de carga (0.789 electrones para el Si) fuera del muffin tin. Esta peque~na cantidad de carga puede distribuirse o bien en el volumen intersticial dejado por los átomos esféricos, dando un fondo de carga intersticial de 0.119 electrones/Å3, o bien distribuida entre la máxima distancia de colisión usada en las simulaciones Monte Carlo y el radio muffin tin. En la figura 5.15 (a), se puede ver una representación de una isosuperficie de densidad constante con cuatro átomos. Parecen esferas desconectadas entre sí, sin nigún enlace.
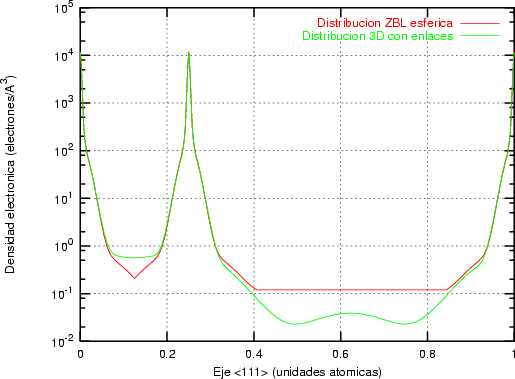
|
Densidad electrónica 3D. Es una densidad de carga de estado sólido que no ha sido promediada y que representa los enlaces Si-Si que existen en la red cristalina perfecta del silicio. Se ha calculado utilizando un método de energía total con pseudo-potenciales ab-initio [89]. Esta densidad se almacena tri-dimensionalmente para el cálculo del frenado electrónico, que se verá afectado por la presencia de los enlaces que estrechan o ensanchan aún más los canales del silicio, dando una descripción mucho más realista. Con la densidad electrónica radial el valor en el interior del canal {110} es constante e igual a 0.119 electrones/Å3, y superior al valor de esta nueva densidad. En la figura 5.16 podemos ver como la composición de las densidades ZBL hace que en la zona intersticial exista una densidad constante, que es superior a la que se obtiene para un cristal periódico 3D. Esto es importante a la hora de describir correctamente el acanalamiento [44, 43]. En el canal {110} este efecto es de suma importancia. En la figura 5.17 vemos sendos cortes de la composición tridimensional de ambas descripciones de la densidad. En el caso ZBL se observa claramente dónde se encuentran los átomos que franquean el canal {110}. Sin embargo, en la densidad 3D, estos no se definen claramente gracias a la presencia de los enlaces Si-Si, lo que dará un frenado más uniforme y menor, evitando el desacanalamiento. En la figura 5.15 (b), se representa una superficie de isodensidad de cuatro átomos de silicio con la densidad de enlaces completos. Se observa que los enlaces están diriguidos correctamente hacia los otros átomos de silicio.
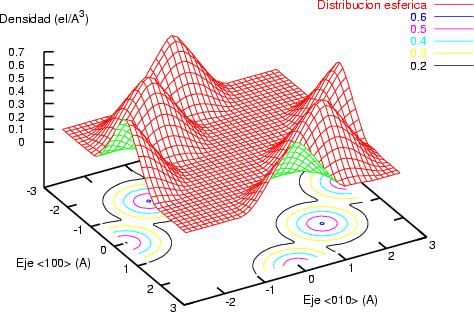
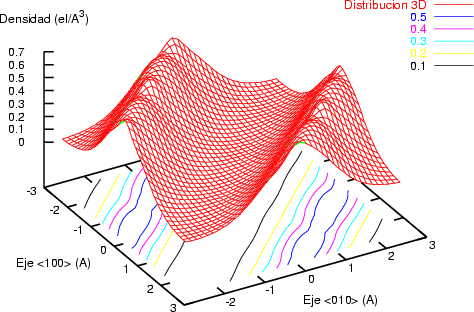
|
Densidad electrónica ISDS. Esta densidad está formada por la superposición de las densidades de átomo aislado que previamente se han calculado con el programa GAMESS [91]. Es una aproximación grosera que en el caso del silicio da unos resultados muy parecidos a los que se obtienen con la densidad 3D con enlaces completos. Sin embargo, pensamos que sólo funcionará aceptablemente bien en el caso de sólidos covalentes no polares [89]. En la figura 5.15 (c), se puede comparar la isosuperficie de densidad de esta descripción con las otras dos descripciones. En este caso, los enlaces se adivinan, aún cuando no tienen la misma forma que con la descripción de enlaces completos.
Modelado y resultados. En nuestro programa se trabaja con densidades 3D, independientemente de la descripción deseada. Si queremos utilizar la densidad radial, simplemente generamos una representación 3D de la misma. Por defecto, se genera una densidad ISDS 3D utilizando densidades radiales de átomo aislado generadas con GAMESS [91]. Para describir correctamente la densidad, se almacena la densidad periódica (del cristal) de una celda básica, que será repetida en todas las direcciones del cristal. En el caso del silicio utilizamos una celda básica de tama~no 5.431 × 5.431 × 5.431 Å3 que está almacenada en una matriz de 112 × 112 × 112 elementos reales. El tama~no de la matriz es de 10.7 Mb7. Necesitaremos una matriz por cada capa distinta de material8.
Hemos hecho un análisis [44, 43] de las diferencias que se obtienen al utilizar las diferentes descripciones de la densidad.
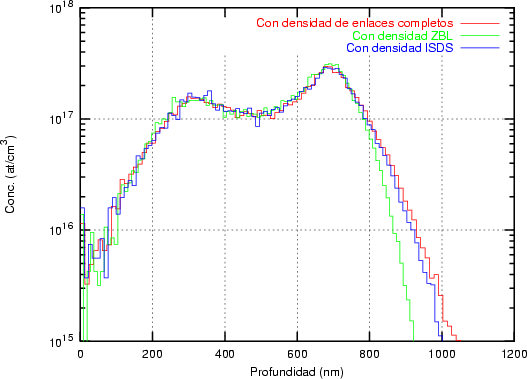
|
En la figura 5.18 observamos el resultado de utilizar las diferentes densidades en el canal {110}. Los resultados con las densidades de enlaces completos e ISDS son similares, mientras que el resultado ZBL difiere de los anteriores. Nuestra conclusión [43] es que en implantaciones acanaladas (canal {110} en el silicio) es importante utilizar una descripción detallada de enlaces completos para poder describir con mayor exactitud la cola del perfil simulado.
En otros trabajos basados en Dinámica Molecular ([8], figura 13), cuando se implanta en este canal se observa que la cola del perfil cae brúscamente ya que utilizan una descripción ZBL de la densidad. Pensamos que en estos programas el uso de la densidad de enlaces completos mejoraría este punto. Sin embargo, el tiempo de cálculo del programa de Dinámica Molecular se vería acrecentado aún más.
Los resultados obtenidos en otros canales no han de variar significativamente, puesto que la descripción ZBL de la densidad lo describe con parecida precisión a la descripción de enlaces completos.
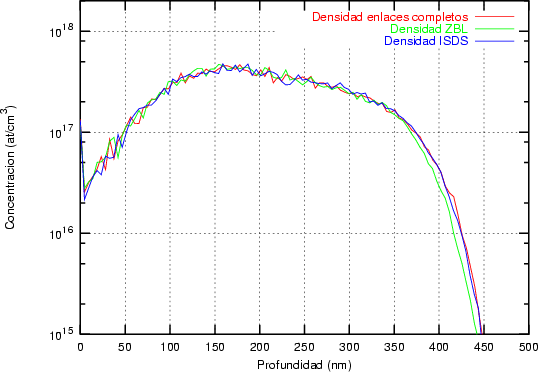 (a) B (7,30)  Si {100} con 35 keV. Si {100} con 35 keV.
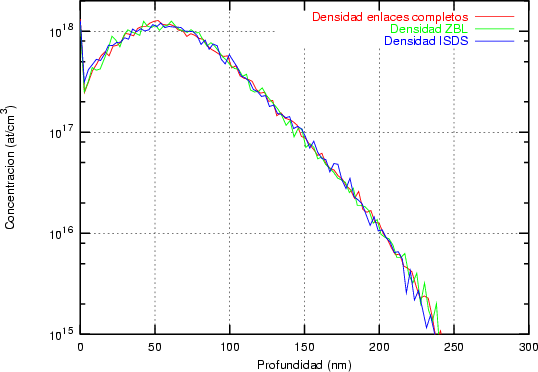 (b) B (0,0)  Si {100} con 15 keV. Si {100} con 15 keV.
|
En las figuras 5.19 (a) y (b) se muestran las comparaciones en las condiciones B(7,30)  Si{100} y B(0,0)
Si{100} y B(0,0)  Si{100}. Notamos que no existen diferencias notables al usar cualesquiera
de las descripciones de la densidad estudiadas.
Si{100}. Notamos que no existen diferencias notables al usar cualesquiera
de las descripciones de la densidad estudiadas.
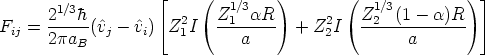 | (5.46) |
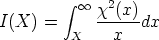 | (5.47) |
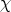 (x) la función de apantallamiento universal ZBL [118], Zi el número atómico,
(x) la función de apantallamiento universal ZBL [118], Zi el número atómico,
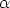 = (1 + (Z2/Z1)1/6)-1 con Z
1 > Z2, R la separación atómica y a = (9
= (1 + (Z2/Z1)1/6)-1 con Z
1 > Z2, R la separación atómica y a = (9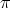 2/128)1/3a
B. Las
velocidades unitarias de proyectil y blanco vienen representadas por
2/128)1/3a
B. Las
velocidades unitarias de proyectil y blanco vienen representadas por 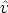 j y
j y 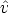 i respectivamente.
Este frenado aumenta cuando la distancia entre Z1 y Z2 disminuye. El valor de la pérdida
energética valdrá entonces:
i respectivamente.
Este frenado aumenta cuando la distancia entre Z1 y Z2 disminuye. El valor de la pérdida
energética valdrá entonces:
 | (5.48) |
Además en este modelo, tal y como menciona Firsov [35], para velocidades del ion suficientemente altas, los electrones de ambos átomos no tendrán el tiempo necesario para interactuar, por lo que la transferencia energética disminuirá. Para tener en cuenta este amortiguamiento en las pérdidas inelásticas más alla de una velocidad crítica (vcritica = 0.7vB) implementamos la siguiente relación [71]:
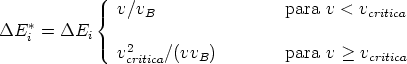 | (5.49) |
Para conseguir una transición suave entre las componentes de alta y baja velocidad, utilizamos la siguiente función de trasferencia descrita en [29]
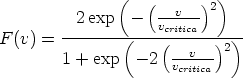 | (5.50) |
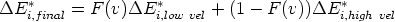 | (5.51) |
La integración de las pérdidas energéticas inelásticas lleva un tratamiento desacoplado del cálculo de las pérdidas nucleares o elásticas. Esto es así debido a que el tratamiento de colisiones simultáneas plantea algunos problemas de dificil resolución, ya que si en el cálculo individual de cada colisión binaria incorporamos la integración de las pérdidas inelásticas, esta será necesariamente a lo largo de las trayectorias reales de las colisiones binarias, que en el caso de colisiones múltiples no se corresponde en ninguna medida con la trayectoria real del proyectil. Además, se contabilizaría más de una vez el frenado electrónico.
En nuestro modelo se integran las pérdidas a lo largo de la trayectoria asintótica del proyectil, formada por tramos rectos. En la figura 5.21 podemos ver una trayectoria típica el la que el proyectil P colisiona secuencialmente con T 1, T 2 y (T 3, T 4), siguiendo tramos rectos. El tratamiento simultaneo consiste en tener en cuenta a todos los átomos blanco que intervienen, cuando se integra. Inicialmente, se resuelve el problema nuclear, ya sea sencillo o simultaneo. A partir de esa resolución se obtienen las posiciones finales de proyectil y blancos, así como una estimación de la energía final de los mismos. A la energía del proyectil se le resta únicamente la transferencia nuclear a los blancos: ETtotal.
A continuación se procede a resolver por separado el cálculo de la integración de las pérdidas por frenado electrónico y de las pérdidas por frenado inelástico. Se tomará el paso de integración apropiado en cada caso para que haya el mínimo error posible y que al mismo tiempo no se invierta mucho tiempo en el cálculo.
Frenado electrónico. La mecánica de integración se puede ver en la figura 5.22. Sabemos que el proyectil avanza desde la posición P 1 hasta la posición P 1', y en el mismo intervalo de tiempo, el átomo blanco recorre el segmento entre T 1 y T 1'. A lo largo del segmento P 1P 1' la energía del proyectil se ve decrementada por las pérdidas Qelect(x) integradas hasta el punto en cuestión, y por la transferencia elástica9 ET (x). Al mismo tiempo se ve afectada por la energía potencial Ep(x) que hay en ese mismo punto, calculada teniendo en cuenta los átomos vecinos, algunos de los cuales están desplazados de sus posiciones de equilibrio (por ejemplo T 1 se va desplazando hasta T 1').
En la figura 5.23 se puede ver la representación de la energía cinética efectiva en función de la distancia recorrida (durante dos tramos rectos, uno de aproximación al blanco y otro de alejamiento). La energía cinética efectiva vale:
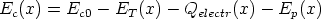 | (5.52) |
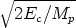 ) y de la densidad electrónica en cada punto. El valor de densidad electrónica
(rs = [3/(4
) y de la densidad electrónica en cada punto. El valor de densidad electrónica
(rs = [3/(4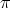
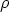 (x))]1/3) que tomamos es estático en cada punto, es decir, el hecho de que los átomos
blanco se desplacen de sus posiciones de cristal perfecto no afecta a la distribución de densidad
electrónica10.
Entonces, tenemos que:
(x))]1/3) que tomamos es estático en cada punto, es decir, el hecho de que los átomos
blanco se desplacen de sus posiciones de cristal perfecto no afecta a la distribución de densidad
electrónica10.
Entonces, tenemos que:
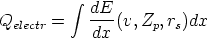 | (5.53) |
Los valores de los parámetros de entrada se escogen de acuerdo con una ley logaritmica. El tama~no de la tabla es:
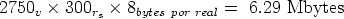 |
|
Frenado inelástico. El cálculo de la integración del frenado inelástico según se comenta en la sección 5.3.2 se realiza siguiendo la trayectoria en tramos rectos del proyectil.
 |
Dado que las pérdidas inelásticas dependen de la distancia entre blanco y proyectil, se integra individualmente cada colisión siguiendo (ver figura 5.24) las asíntotas de aproximación (P 1P 2 para el proyectil y T 1T 2 para el blanco) y alejamiento (P 2P 3 y T 2T 3 para proyectil y blanco respectivamente) entre las dos partículas.
En cada punto de la trayectoria se evalua la pérdida inelástica. Después se suman las diferentes contribuciones individuales, en el caso de una colisión múltiple.
Para aumentar la velocidad de cálculo hemos tabulado la resolución del frenado inelástico en cada punto. Para cada pareja proyectil - blanco (Z1, Z2) generamos una tabla que depende de la distancia entre ambos, R, tomando 1000 puntos y con un rango de variación entre 0 y 15 Å. El tama~no de estas tablas es de
 |
Vuelo libre. Existe una situación especial, que se da cuando los átomos blanco están
demasiado lejos como para colisionar con ellos. Entonces, el programa no detecta ningún blanco
próximo. En ese caso, se hace avanzar al proyectil una cantidad  limit y se vuelve a buscar
blanco.
Es evidente que durante ese vuelo libre el proyectil está sometido al frenado electrónico, que
no al frenado inelástico (despreciable), y se integran las pérdidas electrónicas, sin tener en
cuenta ningún blanco (más sencillo).
limit y se vuelve a buscar
blanco.
Es evidente que durante ese vuelo libre el proyectil está sometido al frenado electrónico, que
no al frenado inelástico (despreciable), y se integran las pérdidas electrónicas, sin tener en
cuenta ningún blanco (más sencillo).
Los mecanismos de integración descritos son muy importantes para conseguir que el programa, con la aproximación BCA, proporcione resultados satisfactorios en condiciones de acanalamiento.
En un primer intento, se consideró apropiado integrar pérdidas electrónicas e inelásticas cuando se calculaban las pérdidas nucleares de forma numérica, como si de un programa de dinámica molecular se tratara. Sin embargo, se vió que no era una solución práctica aplicable en condiciones de acanalamiento en la que aparece el fenómeno de las colisiones simultáneas un buen porcentaje de veces.
El hecho de no tener separadas las diferentes contribuciones de pérdida de energía hacía que no se resolviesen bien los casos de colisiones múltiples. En un replanteamiento del problema decidimos abordarlo en la manera descrita.
| Quien la sigue |
| la consigue |
| ~ Dicho popular ~ |
En este capítulo vamos a hacer una revisión de la predictibilidad de nuestro programa bajo diferentes condiciones de implantación y con diferentes tipos de iones.
Primeramente, en la sección 6.2, revisaremos cual ha sido la parametrización de simulación empleada en todos los casos, para a continuación, en la sección 6.3, comprobar la respuesta del programa en las implantaciones en silicio amorfo, cuando variamos la energía, utilizando diferentes tipos de proyectiles. Compararemos los perfiles obtenidos, con los datos experimentales disponibles y con los resultados obtenidos a través del programa TRIM [118].
En la sección 6.4 comprobaremos como se comporta el programa en el caso de implantaciones en silicio cristalino, probando diferentes canales y energías contrastándolos con los mejores resultados simulados por otros autores hasta el momento, utilizando un modelo con un único parámetro ajustable y el modelo de colisiones binarias. Igualmente contrastaremos nuestros resultados con resultados experimentales obtenidos mediante la técnica SIMS que hemos extraído de la literatura.
El estudio del rango de aplicación del programa en energías y cuáles son las posibles mejoras se aborda en la sección 6.5 donde haremos una crítica constructiva del simulador.
Se han realizado implantaciones simuladas con los iones más interesantes actualmente en tecnología microelectrónica. Sus características aparecen en la tabla 6.1. Se ha supuesto que se escoge el isótopo más abundante de cada especie [59].
|
En la preparación de una simulación existen dos conjuntos de parámetros que hay que definir.
Sin embargo estarán dentro de unos determinados rangos. Hemos selecionado para cada procedencia de los perfiles SIMS unos valores fijos para los mismos. Así empleamos :
Una de las primeras comprobaciones que podemos hacer de la predictibilidad del programa es comprobar los perfiles de impurezas al implantar en silicio amorfo.
En el apéndice B se muestra una colección de comparaciones entre las predicciones del programa y los resultados SIMS, o entre nuestro programa y el resultado de las mismas simulaciones realizadas con el programa TRIM en el caso de implantaciones en silicio amorfo.
Para poder comprobar de un vistazo si nuestro programa predice bien, hemos procesado los perfiles obtenidos. A partir de cada perfil experimental o simulado hemos calculado los momentos de la distribución Pearson IV que se ajusta a ellos (ver sección 3.4). Nuestra intención es comparar el rango proyectado de las implantaciones experimentales y las simuladas.
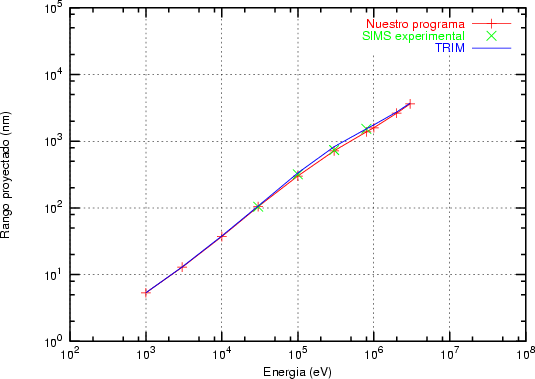
|
Boro. En la figura 6.1 podemos observar la representación de la variación del rango proyectado en función de la energía incidente en el caso de implantar boro en silicio amorfo. Se comparan los perfiles obtenidos con nuestro programa , con TRIM y con algunos resultados experimentales [46]. El valor empleado para rs0 es 1.85, en todos los casos. En el rango de energías medias-bajas el simulador responde muy bien, incluso mejor que TRIM (dato experimental con E = 300 keV). Para energías más altas aparece una ligera diferencia, y no sólo en el caso de implantar en material amorfo. Existe un exceso de frenado en nuestro programa con respecto a TRIM. Pensamos que puede ser debido a un defecto en el modelo físico. Cuando el ion está dentro del material tiene un estado de carga de acuerdo con la velocidad del mismo, siguiendo un valor medio que llamamos curva de ionización (ver sección 5.3.1, ecuación 5.13). Sin embargo, el estado de carga de un ion no puede ser fraccionario2. Un modelizado de las fluctuaciones del estado de carga del ion pueden corregir este problema tal y como comenta Bausells en la referencia [7].
Fósforo. La implantación de fósforo en silicio amorfo se muestra en la figura 6.2. Ambos programas coinciden bastante bien a la hora de determinar el rango proyectado y el perfil en general. Aunque este ion es más pesado que el boro, no necesita un valor de rs0 diferente. Se emplea rs0 = 1.85 (ver Tabla 6.1 en la página 329). Para bajas energías el rango proyectado por nuestro programa se separa del calculado con TRIM. La velocidad del ion es menor al ser más pesado. Esto hace que al ion le de tiempo a interaccionar más en detalle con los átomos que tiene alrededor a lo largo de su trayectoria. Por ello, sería necesario que TRIM incorporase un modelo de colisiones múltiples similar al empleado por nosotros, que sin duda mejoraría sus resultados. Para muy bajas energías nuestro modelo de colisiones simultaneas resulta erroneo. Además la aproximación de colisiones asintóticas deja de ser válida.
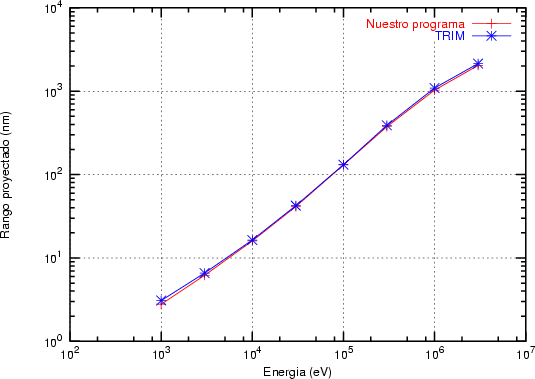
|
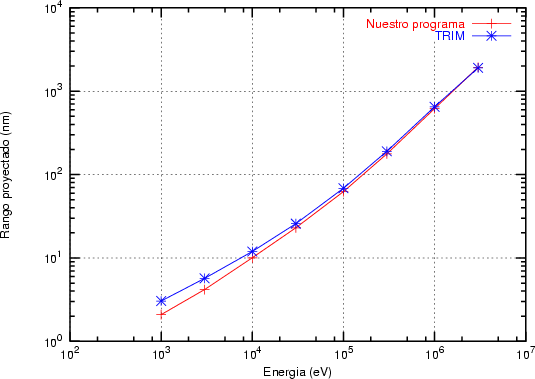
|
Arsénico. En la figura 6.3 realizamos la misma comparación cuando el ion implantado es arsénico. El arsénico es casi siete veces más pesado que el boro. Las diferencias para bajas energías son aún más notables que en el caso anterior. El valor empleado para rs0 es 2.00.
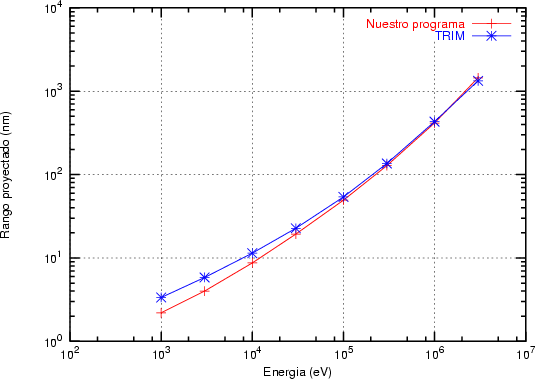
|
Indio. Una última comparación se puede ver en la figura 6.4 en la que el ion implantado es el indio, que es diez veces más pesado que el boro y presenta el mismo comportamiento para bajas energías. En la sección 6.5 analizaremos los límites de aplicación de nuestro programa para bajas y altas energías. El valor de rs0 empleado vale 2.40.
El objetivo fundamental del programa es ser utilizado para simular implantaciones en material cristalino. Todas las simulaciones se han realizado utilizando como material blanco el silicio. En algunos casos está recubierto de una capa de óxido de silicio con un espesor de 15 Å, siempre dependiendo de la información proporcionada junto con los datos experimentales.
 Silicio {100}
Silicio {100}En la figura 6.5 vemos el resultado de tres implantaciones de boro (0,0) en silicio {100} con diferentes energías: 15, 35 y 80 keV. Se observa que las curvas obtenidas con nuestro programa tienen una forma mucho más parecida a los perfiles SIMS que los obtenidos por Cai [19]. No obstante, vemos que la cola de nuestros perfiles se quedan un poco más superficiales que en el perfil experimental:
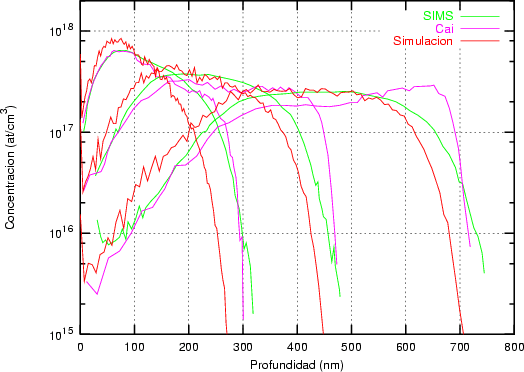
|
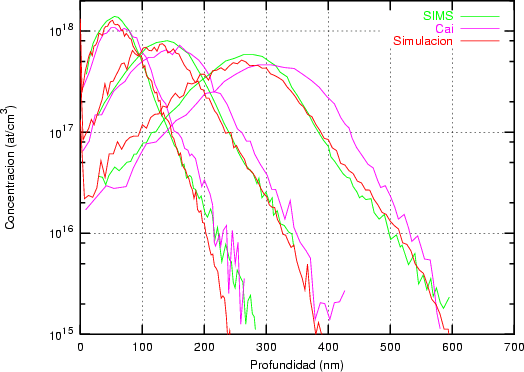
|
 Silicio {100}
Silicio {100}El caso de implantaciones en el canal {100} con parámetros (7,30) aparece en la figura 6.6. Claramente se observa un buen ajuste en el rango proyectado entre nuestro programa y los perfiles SIMS. Los resultados de Cai [19] penetran algo más que el perfil experimental de forma sistemática. Empleamos exáctamente los mismos valores de divergencia, espesor de óxido y temperatura que utilizan en la citada referencia, para poder compararlos.
 Silicio {110}
Silicio {110}Cuando implantamos en el canal más abierto del silicio cristalino, esto es, el canal {110}, observamos (ver figura 6.7) que el segundo pico del perfil, o pico de acanalamiento, es el más problemático. Mientras que los resultados de Cai [19] tienden a quedarse cortos con respecto al resultado experimental, nuestro programa parece entrar algo más.
El primer pico, o pico de amorfo, queda en el mismo sitio con UT-MARLOWE y con nuestro programa , ligeramente más profundos que el perfil SIMS. Un error experimental en profundidad en la medida SIMS, alcanzaría a validar por completo nuestros perfiles.
Sin embargo, también es posible que el modelo de frenado inelástico no sea del todo correcto, sobre todo en el mecanismo de integración, ya que no se integran las pérdidas a lo largo de la trayectoria real, si no sólo a través de una trayectoria en tramos rectos, que no reproduciría la oscilación del proyectil en el canal {110}. Esta oscilación redundaría en un mayor frenado electrónico al pasar por zonas con mayor densidad electrónica como se podía ver en la figura 5.17 de la página 296.
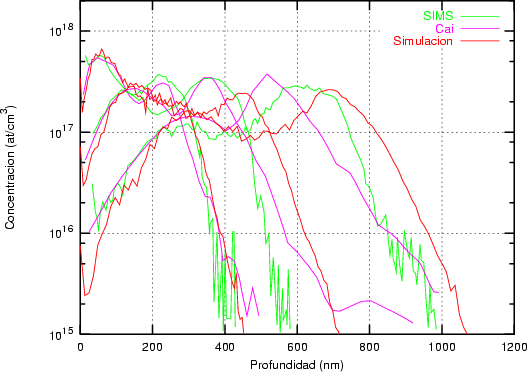
|
Contrastamos en las figuras 6.8 y 6.9 los perfiles simulados al implantar fósforo en el canal {100} con diferentes ángulos, con los perfiles SIMS obtenidos de las referencias [19] y [8] respectivamente. Se observa una buena coincidencia entre ambas parejas de curvas, como era de esperar. El valor de rs0 es 1.85 como en la implantación en silicio amorfo.
La simulación de una implantación en el canal {110} se puede apreciar en la figura 6.10. Hemos de indicar que el perfil SIMS obtenido de la referencia [25] es del a~no 1968, es decir, cuando la técnica SIMS acababa de nacer, por lo que es probable que el error experimental sea mayor que en otras medidas SIMS más modernas. Además carecemos de información acerca de condiciones experimentales como la divergencia del haz, o el espesor del óxido. Hemos supuesto las mismas condiciones que con el resto de simulaciones.
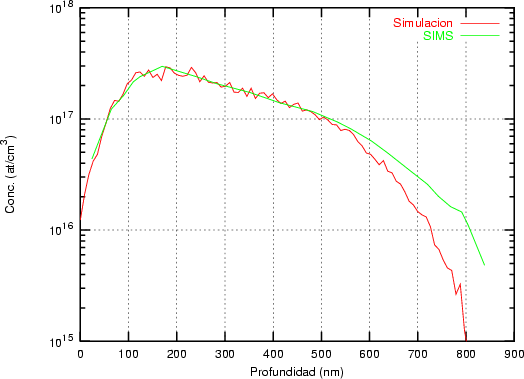
|
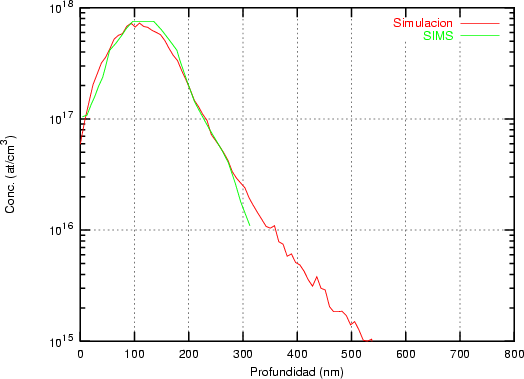
|
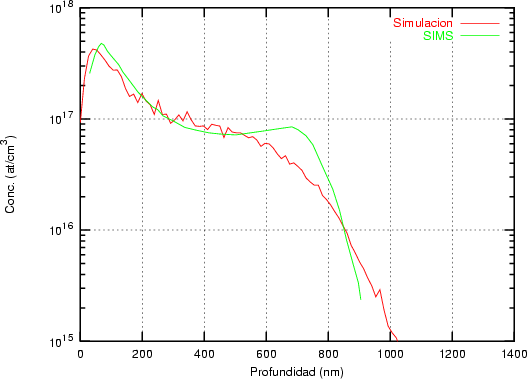
|
El arsénico tiene una masa atómica de 75.000 uma para el isótopo más abundante. En la figura 6.11 vemos una implantación de arsénico (8,30) en silicio {100} con 100 keV. Hasta donde alcanzan los datos experimentales el ajuste es bueno. En el apéndice B existe una colección más amplia de resultados contrastados para el arsénico.
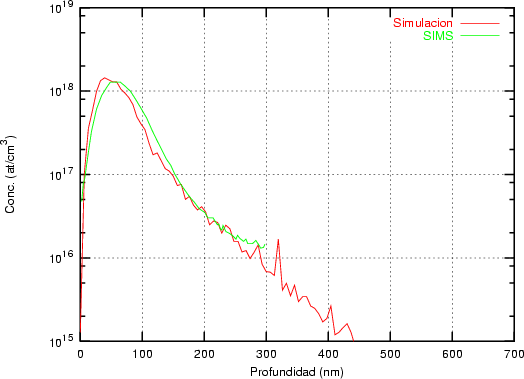
|
El indio es un átomo muy pesado en comparación con los anteriores. Es muy novedoso su empleo en la tecnología microelectrónica, por lo que es complicado encontrar en la literatura perfiles SIMS con los que contrastar los resultados de nuestro programa.
En la figura 6.12 se representan los perfiles experimental y simulado para una implantación de indio (7,22) en silicio {100} con 180 keV. La dosis del perfil experimental era de 2*1013 átomos/cm3 y fue reescalada a 1012 átomos/cm3 para poder comparar.
El desplazamiento observado con respecto al perfil experimental puede deberse a un error en profundidad en la medida SIMS, además del hecho de tratarse de una implantación con una dosis más elevada que la que simulamos, que afectaría a la reducción de la cola de acanalamiento.
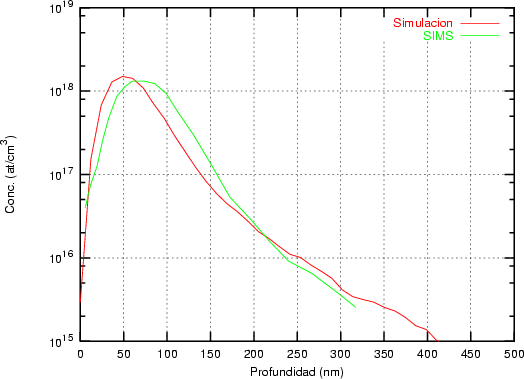
|
En la figura 6.13 aparece la comparación SIMS versus perfil simulado para una implantación de antimonio en silicio. El perfil SIMS, que originalmente tenía una dosis de 4*1012 fue reescalado a 1012 átomos/cm3.
En este caso ocurre algo similar al caso del indio. Si el perfil SIMS lo desplazamos en profundidad se da la coincidencia de ambos perfiles. El problema de la dosis es menos notable, ya que esta es más parecida a la simulada que en el caso del indio.
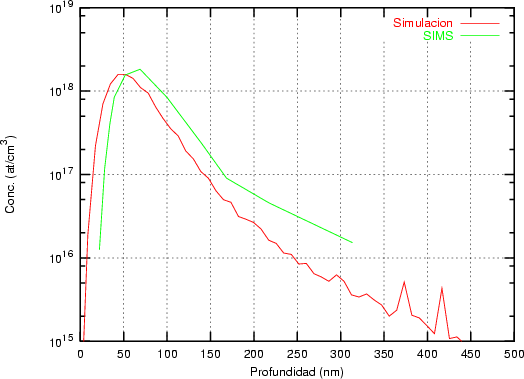
|
En la tabla 6.2 aparece la estimación del rango de validez en energías de nuestro simulador para cada tipo de proyectil. Para ello hemos escalado, el rango inferior inferido para el boro mediante la relación de masas entre el nuevo proyectil y el boro.
La mejora del simulador para bajas energías está seriamente limitada por la precisión que da la aproximación de colisiones binarias. Creemos que sería necesario un mejor modelo de colisiones simultáneas, o incluso una hibridación con dinámica molecular para el caso de bajas energías, con lo que se conseguiría una rápida evolución de las cascadas y que cuando la energía decrezca lo suficiente, quedara bien descrito su comportamiento.
En la tabla 6.2 mostramos los límites calculados para otros proyectiles.
Cuando la energía es más alta, puede ser necesario mejorar el modelo de frenado electrónico para tener en cuenta las fluctuaciones del estado de carga [7], que según Bausells harían que los perfiles simulados entrasen algo más, lo que corregiría el exceso de frenado que observamos en nuestros perfiles.
|
Creemos que nuestro programa cumple el objetivo inicial de ser rápido. Para ello hemos incorporado distintos mecanismos de aceleración de los cálculos, como pueden ser:
El precálculo inicial de las tablas puede llevar algo de tiempo (unos minutos), pero sólo ha de realizarse una única vez, ya que son almacenadas en disco para un uso posterior.
Para hacernos una idea de la velocidad de funcionamiento diría que las simulaciones mostradas en este trabajo y empleando 1 CPU Alpha 21164 a 400 Mhz tardan desde unos minutos a unas horas las de mayor energía (3 MeV, 10 horas ) implantando 10000 iones reales.
El simulador realizado, no está, ni mucho menos, acabado. Siempre se pueden a~nadir caracterísiticas que lo hagan más interesante, y siempre se pueden mejorar los modelos físicos que tiene implementados. Sin embargo, en algún momento hay que faire le point.
No obstante, seguimos trabajando en ello. Actualmente seguimos dos lineas de investigación y desarrollo para mejorar el simulador:
Nuestra idea es desarrollar un nuevo modelo determinista del da~nado que se genera durante la implantación y proceder a su recombinación y difusión siguiendo los novedosos modelos implementados en otro programa (DADOS) desarrollado en este mismo departamento, para conseguir la funcionalidad compuesta a la que se hacía referencia en el International Technology Roadmap for Semiconductor.
Para ello, creemos que se pueden mejorar los modelos de frenado inelástico teniendo en cuenta las fluctuaciones del estado de carga en la linea de lo que dice Bausells en la referencia [7].
| ¿Os dais cuenta de las cosas que tengo que |
| hacer para que me tengáis respeto? |
| ~ atribuida a Alejandro Magno ~ |
En este trabajo hemos hecho un esfuerzo de investigación para conocer y mejorar la técnica de simulación basada en la aproximación de las colisiones binarias, y hemos hecho un esfuerzo de desarrollo al escribir un nuevo programa de simulación que incorpora todas las mejoras.
Con estos algoritmos hemos conseguido reducir el esfuerzo computacional necesario para dar por válida una simulación.
Asímismo se ha desarrollado una versión paralela del código que permite su ejecución en un conjunto heterogéneo de ordenadores conectados en red.
| Si no quieres que nadie se entere, |
| no lo hagas |
| ~ Proverbio chino ~ |
En este apéndice se muestran algunos perfiles de impurezas simulados, variando el proyectil: boro, arsénico, etc., y variando las condiciones de implantación: energía, amorfo/cristalino, orientación cristalográfica, ángulos cenital (tilt) y azimutal (rotación), etc. para comprobar el funcionamiento del mismo. Todos los perfiles experimentales que se han usado tienen una dosis de implantación baja, para poder aplicar el simulador, sin embargo, los perfiles experimentales tienen dosis variables aunque peque~nas (< 1014), que han sido reescaladas a 1012 átomos/cm2.
Acceso a un resultado. Para cada tipo de proyectil hemos generado una tabla que hace referencia a las diferentes condiciones de implantación probadas. Ver tabla B.1 para el boro y tabla B.2 para el arsénico.
Notacion. En las gráficas se representa en el eje de abcisas la profundidad alcanzada medida en nanometros, y en el eje de ordenadas la concentración de impurezas medida en átomos/cm3. El resultado de la simulación de nuestro programa se representa en color rojo , mientras que los resultados experimentales obtenidos por la técnica SIMS aparecen en color verde. Cuando se representan perfiles de implantación en materiales amorfos, en la mayoría de los casos se compara con el resultado del simulador TRIM, y la curva aparece en color azul.
|
|
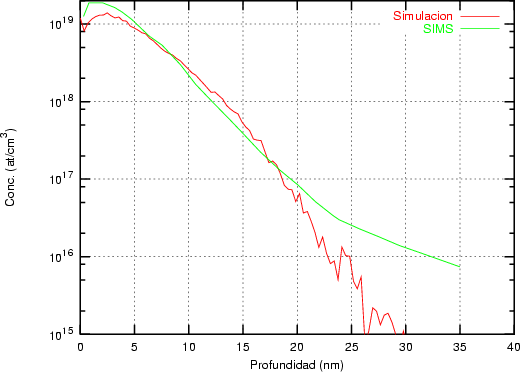
|
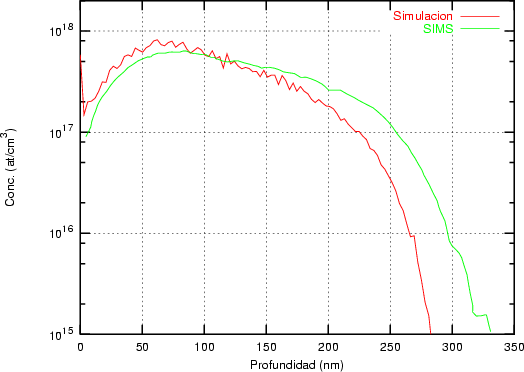
|
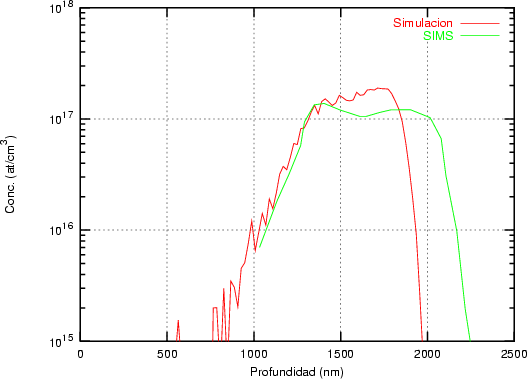
|
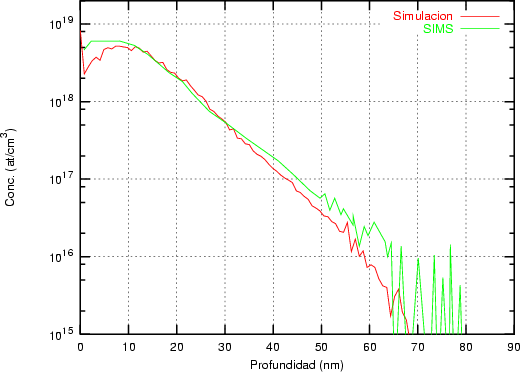
|
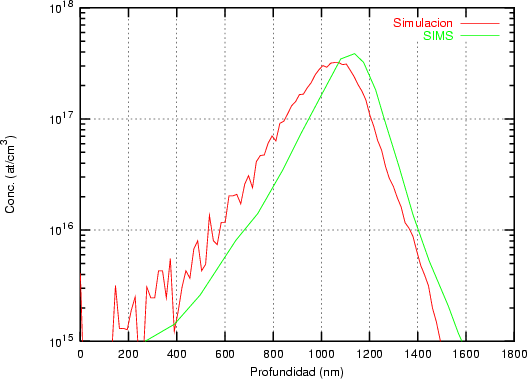
|
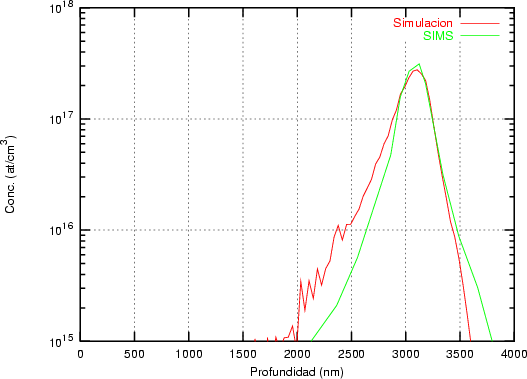
|
En esta sección me gustaría mostrar al lector algunos perfiles bidimensionales obtenidos con el simulador. No tenemos datos experimentales para contrastarlos, sin embargo, es una buena manera de comprobar que no sucenden cosas extra~nas.
En silicio amorfo. Es interesante comprobar como queda lateralmente una implantación en material amorfo, sobre todo para verificar el correcto funcionamiento del modelizado del material, comprobando que no aparece el acanalamiento. En la figura B.31 se representa un perfil simulado bidimensional de una implantación de boro en silicio con 10 keV. Las curvas representan isoniveles de concentración. No se observa el efecto del acanalamiento1 como era de esperar.
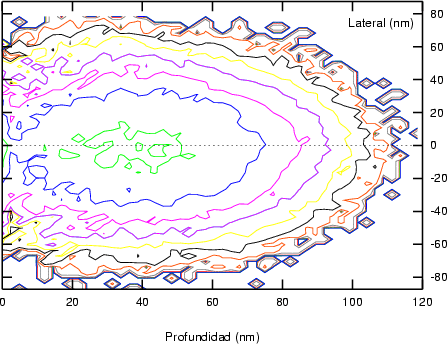
|
En silicio cristalino. El acanalamiento de los iones en las diferentes condiciones de implantación a través de perfiles bidimensionales de impurezas da una visión diferente de lo que ocurre en el semiconductor. Además es uno de los puntos a desarrollar según la Semiconductor Industry Association. Incluso en algún perfil puede verse el acanalamiento por planos. En la figura B.32 representamos un perfil bidimensional en el canal {100} implantando directamente en él (tilt=0). Se observa el canal claramente. Lateralmente no aparecen otros canales, ya que es poco probable que se desacanale.
En la figura B.33 implantamos en el mismo canal pero con una cierta desviación (tilt=7), tal y como se implanta en la realidad para evitar el acanalamiento, sin embargo, se observa que algunos iones sí se acanalan.
Y por último, en la figura B.34 estudiamos el acanalamiento cuando implantamos en el canal más abierto del silicio, el {110}. Los dos máximos aparecen claramente, sufriendo el segundo un fuerte encajonamiento.
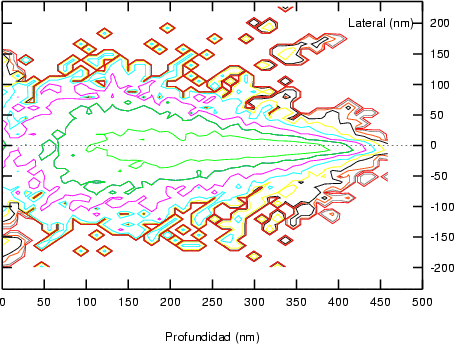
|
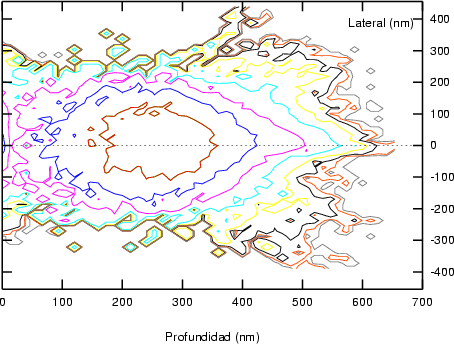
|
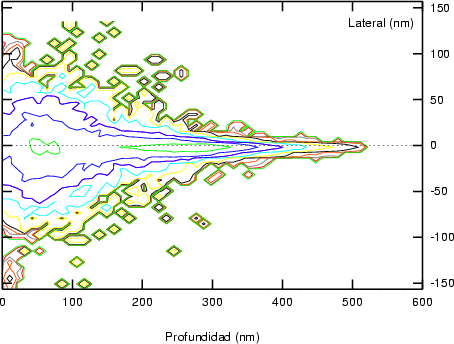
|
| Por la ignorancia nos equivocamos |
| y por las equivocaciones aprendemos |
| ~ Proverbio romano ~ |
En este apéndice se describen las palabras claves que se pueden introducir en el fichero de entrada de nuestro programa para describir las condiciones de la implantación iónica que se quieren simular así como seleccionar las opciones de funcionamiento y salidas gráficas o ficheros que se desean.
El texto que viene a continuación está escrito en inglés, en un intento de hacer que el duro trabajo de describir las palabras clave del programa sea más sencillo, al hacerlo una única vez. De esta manera podrá servir a otras personas, en un ámbito internacional, interesadas en manejarlo. Ruego, por tanto, al lector que me disculpe.
This is an example file to describe all the features implemented in the current version (2000.04.12) of the Ion Implantation In Semiconductors (I3S) program. The introduction of parameters is very simple. You must only write the correct (case sensitive) keyword in the input file and the values assigned to. The quantities shown with [ ] are used by default if the keyword does not appear. If some keyword appears twice or more times in the file, the program take the last value assigned to.
Atom Name(up to 2 chars) AtomicNumber AtomicMass(in uma) DebyeTemp
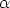 ,
, 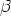 ,
, 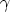 ). In degrees.
). In degrees.
XTtal NAtom Type Xpos Ypos Zpos BindingEnergy
where NAtom is the index of the atom (i.e.: 2=Si, 3=O ) as you have introduced before. Type is the centered type. You can choose from: (1) primitive, (2) body centered, (3) A end centered, (4) B end centered, (5) C end centered, (6) face centered. Xpos Ypos Zpos are the relative coordinates measured in lattice parameter units referred to the unit cell origin. BindingEnergy is the energy needed to move out an atom from his lattice site (in eV).
// Define a layer of Si //
Amorphous 0
LatticeParameter 5.431 5.431 5.431
Angles 90.0 90.0 90.0
XTal 2 6 0.00 0.00 0.00 15
XTal 2 6 0.25 0.25 0.25 15
XMin 15.0 A
XMax 1e10
EDTCreate 0
EDTFile[ EDT_Si ]
|
The value is the sum of the following:
(+1) show the projectile (proj.xyz)
(+2) show the touched atoms and interst. generated (interst.xyz)
(+4) show the targets selected in each collision (targets.xyz)
(+8) show the xtal (xtal.xyz)
|
(+1) projectile info
(+2) interst. info
(+4) targets info
(+8) xtal info
(+16) cascade info
(+32) detailed info
(+64) init pos info
(+128) phonons info
(=52) max detail
|
Dentro del fichero de entrada se pueden escribir los comentarios que se quiera, teniendo cuidado de no emplear las palabras clave RS0 2.40 RareEvent 2 HST 1 HSTFile[ In_a_100_0. ] GPPlot[ t"Simulacion","SIMS/in_a_100.trim"t"TRIM" ] GPInit[ set yrange[1e15:] ] ENERGY 100000 eV NumberOfImplants 10000 Tha 0 degrees (tilt) Phi 0 degrees Divergence 0.5 degrees ABC 1 0 0 Therm 1 Temperature 300 kelvin Atom In 49 115.00 519.0 Atom Si 14 28.086 519.0 AtomP 1 // Defino la capa de Si <100> XTal 2 6 0.00 0.00 0.00 15 // Si XTal 2 6 0.25 0.25 0.25 15 // Si Amorphous 2 XMin 0.0 A XMax 1e10 A EDTFile[ EDT_Si ] |
RS0 1.85 Divergence 0.5 degrees RareEvent 2 HST 1 HSTFile[ B_110_80. ] GPPlot[ t"Simulacion","SIMS/b110_80.dat"t"SIMS" ] GPInit[ set yrange[1e15:2e18] ] ENERGY 80000 NumberOfImplants 10000 ABC 1 1 0 Tha 0 degrees (tilt) Phi 0 degrees Therm 1 Temperature 300 kelvin Atom B 5 11.000 519.0 Atom Si 14 28.086 519.0 Atom O 8 15.994 519.0 AtomP 1 // SiO2 (amorfo) LatticeParameter 4.91304 4.91304 5.40463 Angles 90.0 90.0 60.0 XTal 2 1 0.3333 -0.465 -0.465 15 // Si XTal 2 1 0.0 0.0 0.465 15 // Si XTal 2 1 0.6666 0.465 0.0 15 // Si XTal 3 1 0.12 0.272 0.415 15 // O XTal 3 1 0.4533 -0.415 -0.143 15 // O XTal 3 1 0.7866 0.143 -0.272 15 // O XTal 3 1 -0.12 -0.272 0.143 15 // O XTal 3 1 0.5467 0.415 0.272 15 // O XTal 3 1 0.2133 -0.143 -0.415 15 // O Amorphous 2 XMin 0 A XMax 15.0 A NextLayer // Si <100> XTal 2 6 0.00 0.00 0.00 15 // Si XTal 2 6 0.25 0.25 0.25 15 // Si Amorphous 0 XMin 15.0 A XMax 1e10 A EDTFile[ EDT_Si ] |
[1] S. Ahmed, C.J. Barbero, T.W. Sigmon, and J.W. Erickson. Empirical depth profile
simulator for ion implantation in 6H -SiC. J. Appl. Phys., 77(12):6194-6200, 1995.
-SiC. J. Appl. Phys., 77(12):6194-6200, 1995.
[2] J. Arias. Simulación de la implantación iónica en cristales incluyendo baja energia y acumulación de da~nado. PhD thesis, Universidad de Valladolid, Valladolid, 1995.
[3] J. Arias, J. Hernández, M. Jaraiz, L. Bailón, and J. Barbolla. Accurate computer simulation of ion implantation in crystalline silicon. In Conferencia de Dispositivos Electrónicos, Barcelona, 1997.
[4] J. Arias, M. Jaraiz, L. Pelaz, L. Bailón, and J. Barbolla. Low energy implantation simulation using a modified binary collision aproximation code. Nucl. Instr. and Meth. B, 102:228-231, 1995.
[5] J. Arias, M. Jaraiz, J.E. Rubio, L. Pelaz, L.A. Marqués, and J. Barbolla. Detailed computer simulation of ion implantation processes into crystals. Journal Mat. Sci. and Tech., 11:1191-1193, 1995.
[6] R. Azziz, K.W. Brannon, and G.R. Srinivasan. Electronic stopping power for low energy ions. In Mat. Res. Soc. Symp. Proc., 1985.
[7] J. Bausells. Effect of charge-state fluctuations of ions moving in solids on high-energy ion implantation. J. Appl. Phys., 69(1):155-161, 1991.
[8] Keith M. Beardmore and Niels Gronbech-Jensen. Efficient molecular dynamics scheme for the calculation of dopant profiles due to ion implantation. Phys. Rev. E, 57(6):7278-7287, 1998.
[9] A. Benninghoven, F.G. R¨uenauer, and H.W. Werner. Secondary Ion Mass Spectroscopy: Basic concepts, Instrumental Aspects, Applications, and Trends. Wiley, New York, 1987.
[10] H.A. Bethe. Ann. Phys. (N.Y.), 5:325, 1930.
[11] M. Blackman. Handbuch der physik, volume 7. Springer-Verlag, Berlin, 1955.
[12] W. Bohmayr, A. Burenkov, J. Lorenz, H. Ryssel, and S. Selberherr. Trajectory split method for Monte Carlo simulation of ion implantation. IEEE Trans. Semic. Manuf, 8(4):402-407, 1995.
[13] N. Bohr. Phys. Rev., 58:654, 1940.
[14] N. Bohr. Phys. Rev., 59:270, 1941.
[15] A. Bousetta, J.A. van der Berg, D.G. Armour, and P.C. Zalm. Si ultrashallow p + n junctions using low-energy boron implantation. Appl. Phys. Lett., 58(15):1622-1628, 1991.
[16] A. Brand, A. Haranahalli, N. Hsieh, Y.C. Lin, G. Sery, N. Stenton, B.J. Woo, S. Ahmed, M. Bohr, S. Thompson, and S. Yang. Intel’s 0.25 micron, 2.0 volts logic process technology. Intel Technology Journal, 3, 1998.
[17] Werner Brandt and M. Kitagawa. Effective stopping-power charges of swift ions in condensed matter. Phys. Rev. B, 25(9):5631-5637, 1982.
[18] G. Buschhorn, E. Diedrich, W. Kufner, M. Rzepka, H. Genz, P. Hoffmann-Stascheck, and A. Richter. Temperature dependence of planar channeling radiation in silicon, germanium, and beryllium between 12 and 333 K. Phys. Rev. B, 55(10):6196-6202, 1997.
[19] David Cai, Niels Gronbech-Jensen, C.M. Snell, and K.M. Beardmore. Phenomenological electronic stopping-power model for molecular dynamics and Monte Carlo simulation of ion implantation into silicon. Phys. Rev. B, 54(23):17147-17157, 1996.
[20] David Cai, C.M. Snell, Keith M. Beardmore, and N. Gronbech-Jensen. Simulation of phosphorous implantation into silicon with a single parameter electronic stopping power model. Int. J. Modern Physics C, 9(3):459-470, 1998.
[21] I.R. Chakarov and R.P. Webb. Computer simulation of B, P and As channeling profiles in silicon. In Cosires, 1992.
[22] S.C. Chapra. Numerical methods for engineers with personal computer applications. McGraw-Hill, EEUU, 1985.
[23] Y. Chen, B. Obradovich, M. Morris, G. Wang, J. Balamurugan, D. Li, A.F. Tasch, D. Kamenitsa, W. McCoy, S. Baumman, D. Sieloff, D. Dyer, and P. Zeitroff. Monte Carlo simulation of heavy species (indium and germanium) ion implantation into silicon. http://tcad.stanford.edu/tcad-journal/archive, 1999.
[24] Sonu Daryanani, Jim Jillson, and Ronald Eddy. Issues in the ion implantation of Si for GaAs applications. III-Vs review, 10(2):26-31, 1997.
[25] G. Dearnaley, J.H. Freeman, and J. Stephen. Can. Journal of Physics, 46:587, 1968.
[26] Ruth DeJule. New designs in high-current ion implanters. Semiconductor International, 21(4), 1998.
[27] M. Deustch and M. Hart. Phys. Rev. B, 31:3846, 1985.
[28] J. Dongarra, A. Geist, R. Mancheck, and V. Sunderman. Integrated PVM framework supports heterogeneous network. Computer in Physics, 7(2):166-175, 1993.
[29] M.J. Dort, P.H. Woerlee, and A.J. Walker. Solid State Electronics, 37(3):411-414, 1994.
[30] A. Dygo, P.J.M. Smulders, and D.O. Boerma. Simulation analysis of ion channeling spectra: thermal vibrational amplitude in Si. Nucl. Instr. and Meth. B, 64:701-705, 1992.
[31] P.M. Echenique, R.M. Nieminen, J.C. Ashley, and R.H. Ritchie. Nonlinear stopping power of an electron gas for slow ions. Phys. Rev. A, 33(2):897-904, 1986.
[32] P.M. Echenique, R.M. Nieminen, and R.H. Ritchie. Density functional calculation of stopping power of an electron gas for slow ions. Solid State Communications, 37:779-781, 1981.
[33] L. Enriquez, M. Jaraiz, J. Hernández, J. Barbolla, S. Libertino, and S. Coffa. Difussion, clustering and trapping of point defects in ion implanted silicon: atomistic simulation and experiments. In Conferencia de Dispositivos Electrónicos, Barcelona, 1997.
[34] L. Enriquez, M. Jaraiz, J. Hernández, J. Barbolla, S. Libertino, and S. Coffa. Difussion, clustering and trapping of point defects in ion implanted silicon: atomistic simulation and experiments. In Mat. Res. Soc. Symp. Proc., San Francisco, 1997.
[35] O.B. Firsov. A qualitative interpretation of the mean electron excitation energy in atomic collisions. Sov. Phys. JETP, 36:1076-1080, 1959.
[36] Ron Fleming. Theory and Instrumentation Tutorials for SIMS and RBS. http://www.cea.com, 1995.
[37] Konrad Gartner, Mirko Nitschke, and Wolfgang Eckstein. Computer simulation studies of low energy B implantation into amorphous and crystalline silicon. Nucl. Instr. and Meth. B, 83:87-94, 1993.
[38] V. Ghante, L.M. Lam, S. Morris, S.H. Yang, A.F. Tasch, D. Kamenitsa, J. Sheng, and C. Magee. The detailed dependence of implanted phosphorous profiles in (100) single-crystal Si on key implant parameters. In Mat. Res. Soc. Symp. Proc., 1996.
[39] M.D. Giles. Ion implantation calculations in two dimensions using the Boltzman transport equation. Trans. on Computer-Aided Design of Integrated Circuits, 5(4):679-684, 1986.
[40] Paul Glasserman, Phillip Heidelberger, Perwez Shahabuddin, and Tim Zajic. Multilevel splitting for estimating rare event probabilities. Technical report, IBM, 1996.
[41] J.M. Haile. Molecular dymanics simulation: elementary methods. John Wiley and sons, Inc., New York, 1992.
[42] C. Hastings. Approximations for digital computers. Princeton university press, New Jersey, 1955.
[43] J. Hernández, M. Jaraiz, J. Arias, L. Bailón, J. Barbolla, A. Rubio, and J.L. Orantes. Effect of silicon bonds on channelling implant simulations. In Conferencia de Dispositivos Electrónicos, Madrid, 1999.
[44] J. Hernández, M. Jaraiz, J. Arias, J. Barbolla, L. Bailón, and A. Rubio. Effect of silicon bonds on channelling implant simulations. In Mat. Res. Soc. Symp. Proc., San Francisco, 1998.
[45] G Hobler, A. Simionescu, L Palmetshofer, F. Jahnel, R. von Criegern, C. Tian, and G. Stingeder. Verification of models for the simulation of boron implantation into crystalline silicon. Journal Vac. Sci. and Tech. B, 14:272-277, 1996.
[46] W.K. Hofker. Implantation of boron in silicon. Phillips Res. Repts. Suppl, 8, 1975.
[47] Mark Hou and Mark T. Robinson. Computer studies of low energy scattering in crystalline and amorphous targets. Nucl. Instr. and Meth., 132:641-645, 1976.
[48] G.A. Huber and S. Kim. Weighted-ensemble Brownian dynamics simulations for protein association reactions. Biophysical journal, 70:97-110, 1996.
[49] M. Jaraiz, J. Arias, L.A. Bailón, and J. Barbolla. Detailed computer simulation of damage accumulation in ion irradiated crystalline targets. Vacuum, 44:321-323, 1993.
[50] M. Jaraiz, J. Arias, J.E. Rubio, L.A. Bailón, and J. Barbolla. Computer simulation of point-defect distributions generated by ion implantation. Nucl. Instr. and Meth. B, 80:172-175, 1993.
[51] J.O. Kephart, B.L. Bernman, R.H. Pantell, S. Datz, R.K. Kein, and H. Park. Thermal-vibrational amplitudes of silicon determined by channeling-radiation measurements. Phys. Rev. B, 44(5):1992-2002, 1991.
[52] L.M. Kishinevskii. Bull. Acad. Sci. USSR, Phys Ser, 26:11433, 1962.
[53] Charles Kittel. Introducción a la física del estado sólido. Reverté, Barcelona, 1993.
[54] Kevin M. Klein, Changae Park, and A.F. Tasch. Monte Carlo simulation of boron implantation into single-crystal silicon. IEEE Trans. Elect. Dev., 39(7):1614-1621, 1992.
[55] K.M. Klein, C. Park, and A.F. Tasch. Local electron concentration-dependent stopping power model for Monte Carlo simulation of low-energy ion implantation in silicon. Appl. Phys. Lett., 57(25):2701-2703, 1990.
[56] K.M. Klein, C. Park, and A.F. Tasch. Modeling of cumulative damage effects on ion implantation profiles. Nucl. Instr. and Meth. B, 59/60:60-64, 1991.
[57] S. Kreussler, C. Varelas, and W. Brandt. Phys. Rev. B, 23(82), 1981.
[58] W.E. Lamb. Phys. Rev., 58:696, 1940.
[59] G.J. Leigh. Nomenclature of inorganic chemistry. Blackwells Scientific Publications, Oxford, 1990.
[60] W. Lenz. Z.f. Physik, 77:713, 1947.
[61] J. Lindhard and M. Scharff. Energy dissipation by ions in the keV region. Phys. Rev., 124:128-130, 1961.
[62] J. Lindhard, M. Scharff, and H.E. Schiott. Range concepts and heavy ion ranges. Dan. Vidensk. Seksk. Mat. Fys. Medd., 33(14):1-42, 1963.
[63] J. Lindhard and A.K. Winther. Dan. Vidensk. Seksk. Mat. Fys. Medd., 34:4, 1964.
[64] Teng-Cai Ma, You-Nian Wang, and Tao Cui. Numerical evaluation of the stopping power for a proton in a strongly coupled electron gas. J. Appl. Phys., 72(8):3838-3840, 1992.
[65] Ady Mann and Werner Brandt. Material dependence of low-velocity stopping powers. Phys. Rev. B, 24(9):4999-5003, 1981.
[66] J.B. Marion. Classical dynamics of particles and systems. Academic Press, Inc., New York, 1986.
[67] L.A. Marqués, J.E. Rubio, M. Jaraiz, J. Arias, L. Pelaz, and J. Barbolla. Dechanneling by thermal vibrations in silicon ion implantation. In Ion implantation technology-94, Catania, Italy, 1995.
[68] Richard J. Mathar. The Brand-Kitagawa heavy ion model: Embedding in the homogeneous electron gas. Nucl. Instr. and Meth. B, 132:18-28, 1997.
[69] Richard J. Mathar and Matthias Posselt. Effective-charge theory for the electronic stopping of heavy ions in solids: Stripping criteria and target-electron models. Phys. Rev. B, 51(1):107-116, 1995.
[70] G. Moliere. Z.f. Naturforsch, A2:133, 1947.
[71] S. Morris, D. Lin, S.H. Yang, S. Tian, K. Parab, and A.F. Tasch. Development and demonstration of a two-dimensional accurate and computationally-efficient model for boron implantation into single-crystal silicon through overlying oxide layers. In Mat. Res. Soc. Symp. Proc., 1996.
[72] S. Morris, B Obradovich, S.H. Yang, A.F Tasch, and L. Rubin. An electronic stopping power model in single-crystal silicon from a few KeV to several MeV. In Mat. Res. Soc. Symp. Proc., 1996.
[73] E. Morvan, P. Godignon, S. Beberich, M. Vellvehi, and J. Millán. Electronic stopping power for Monte Carlo simulation of ion implantation into SiC. Nucl. Instr. and Meth. B, 147:68-73, 1999.
[74] Cheruvu S. Murthy and G.R. Srinivasan. Computer simulation studies of ion implantation in crystalline silicon. IEEE Trans. Elect. Dev., 39(2):264-273, 1992.
[75] L.~Nesbit et al. Journal of Electrochemical Society, 133:1186, 1986.
[76] Oak Ridge National Laboratory. PVM Library. http://www.netlib.org/pvm3/, 1999.
[77] O.S. Oen and M.T. Robinson. J. Appl. Phys., 46:5069, 1975.
[78] K.B. Parab, S.H. Yang, S.J. Morris, S. Tian, M. Morris, B. Obradovich, A.F. Tasch, D. Kanemitsa, R. Simonton, and C. Magee. Detaild analysis and computationally efficient modeling of ultra-shallow dopant profiles obtained by low energy B, BF 2 and As ion implantation. In Mat. Res. Soc. Symp. Proc., 1996.
[79] Changae Park, Kevin M. Klein, and A.F. Tasch. Efficient modelling parameter extraction for dual Pearson approach to simulation of implanted impurity profiles in silicon. Solid State Electronics, 33(6):645-650, 1990.
[80] L. Pelaz, M. Jaraiz, G. H. Gilmer, H.J. Gossmann, C. S. Rafferty, D. J. Eaglesham, and J. M. Poate. B diffusion and clustering in ion implanted Si: The role of B cluster precursors. Appl. Phys. Lett., 70(17):2285-2287, 1998.
[81] Matthias Posselt, Bruno Schmidt, THomas Feudel, and Norbert Strecker. Atomistic simulation of ion implantation and its application in Si technology. Materials Science Engineering B, 71:128-136, 2000.
[82] Helmut Puchner. Advanced process modelling for VLSI Technology. PhD thesis, Technischen Universitat Wien, Wien, 1996.
[83] V. Raineri, V. Primitera, G. Galvagno, F. Priolo, and E. Rimini. Channeling implants in silicon crystals. Materials Chemistry and Physics, 38:105-130, 1994.
[84] Mulpuri V. Rao, J.A. Gardner, P.H. Chi, O.W. Holland, G. Keiner, J. Kretchmer, and M. Grezzo. Phosphorous and boron implantation in 6H-SiC. J. Appl. Phys., 81(10):6635-6641, 1997.
[85] R.H. Ritchie. Phys. Rev., 114:664, 1959.
[86] Mark T. Robinson. Slowing-down time of energetic atoms in solids. Phys. Rev. B, 40(16):10717-10726, 1989.
[87] Mark T. Robinson and Ian M. Torrens. Computer simulation of atomic-displacement cascades in solids in the binary-collision approximation. Phys. Rev. B, 9(12):5008-5024, 1974.
[88] M.T. Robinson. MARLOWE. Binary collision cascade simulation program version 12. User’s guide. Radiation Shielding Information Center, ORNL, Oak Ridge, TN 37831-6362, pages 1-115, 1984.
[89] Angel Rubio. Comunicación privada. Dpto. Física Teórica, Facultad de Ciencias, Univ. de Valladolid, 1997.
[90] S. E. Hansen and M. D. Deal. SUPREM-IV.GS. User’s manual. Integrated Circuits Laboratory. Stanford University. Stanford, California 94305, 1994.
[91] M.W. Schmidt, K.K. Baldridge, J.A. Boatz, S.T. Elbert, M.S. Gordon, J.J. Jensen, S. Koseki, N. Matsunaga, K.A. Nguyen, S. Su, T.L. Windus, M. Dupuis, and J.A. Montgomery. GAMESS. General Atomic and Molecular Electronic Structure System. J.Comput.Chem., 14:1347-1363, 1993.
[92] W. Shockley. Forming semiconductor devices by ionic bombardment. US Patent 2787564. Technical report, Bell Laboratories, 1954.
[93] W.L. Smith, A. Rosenawaig, D.L. Willenborg, J. Opsal, and M.W. Taylor. Solid State Technology, 85:85-92, 1986.
[94] A. Sommerfeld. Z.f. Physik, 77:722, 1932.
[95] I.A. Stegun. Handbook of mathematical functions. National bureau of standards, Washington, 1964.
[96] F.H. Stillinger and T.A. Weber. Computer simulation of local order in condensed phases of silicon. Phys. Rev. B, 31(8):5262-5271, 1985.
[97] V. Sunderman, J. Dongarra, A. Geist, and R. Mancheck. The PVM concurrent computing system: evolution, experiences and trends. Parallel Computing, 20(4):531-547, 1994.
[98] S.M. Sze. VLSI Technology. McGraw-Hill, New Jersey, 1983.
[99] S.M. Sze. Semiconductor Device Physics and Technology. Willey, New York, 1985.
[100] A.F. Tasch, S.H. Yang, S.J. Morris, S. Tian, K. Parab, D. Kamenitsa, C. Magee, Novak, and G. Lux. Ion implant modeling for ULSI integrated circuits. Semiconductor International, pages 95-104, 1995.
[101] J. Tersoff. New empirical model for the structural properties of silicon. Phys. Rev. Lett., 56(6):632, 1986.
[102] J. Tersoff. Empirical interatomic potential for silicon with improved elastic properties. Phys. Rev. B, 38(14):9902-9905, 1988.
[103] J. Tersoff. New empirical approach for the structure and energy of covalent systems. Phys. Rev. B, 37(12):6991-7000, 1988.
[104] Therma-Wave. Therma Wave Inc. Fremont, CA 94539, USA. http://www.thermawave.com, 1999.
[105] S. Tian, S.-H. Yang, S. Morris, K. Parab, A.F. Tasch, D. Kamenitsa, R. Reece, B. Freer, R.B. Simonton, and C. Magee. The effect of dose rate on ion implanted impurity profiles in silicon. In Electronics Materials Conference, Charlottesville, VA, 1995.
[106] P.D. Townsend, J.C. Kelly, and N.E.W. Hartly. Ion implantation, sputtering and their applications. Academic, New York, 1976.
[107] Texas University of Austin. UT-MARLOWE 5.0 User’s guide. http://homer.mer.utexas.edu/TCAD/utmarlowe, 1999.
[108] Kenichi Utsumi and Setsuo Ichimaru. Dielectric formulation of strongly coupled electron liquids at metalic densities. analitic expresion for the local-field correction. Phys. Rev. A, 26(1):603-610, 1982.
[109] You-Nian Wang and Teng-Cai Ma. Electronic stopping power for slow atoms in solids. Phys. Rev. A, 44(3):1768-1772, 1991.
[110] Karl Wimmer. Two-dimensional non planar process simulation. PhD thesis, Technischen Universitat Wien, Wien, 1993.
[111] Robert H. Wolfe, Mark Needels, Tomas Arias, and John D. Joannopoulos. Visual revelations from silicon ab initio calculations. IEEE Computer Graphics and Applications, 0:45-53, July 1992.
[112] S.H. Yang. Monte carlo simulation of arsenic ion implantation into single-crystal silicon. PhD thesis, University of Texas, Austin, 1995.
[113] S.H. Yang, D. Lim, S.J. Morris, and A.F. Tasch. Improved efficiency in Monte Carlo simulation of ion implanted impurity profiles in single-crystal materials. Nucl. Instr. and Meth. B, 102:242-246, 1995.
[114] S.H. Yang, S. Morris, S. Tian, K. Karab, A.F. Tasch, P.M. Echenique, R. Capaz, and J. Joannopoulos. A new electronic stopping model for the Monte Carlo simulation of arsenic ion implantation into (100) single-crystal silicon. In Mat. Res. Soc. Symp. Proc., 1995.
[115] S.H. Yang, S.J. Morris, D.L. Lim, A.F. Tasch, R.B. Simonton, D. Kamenitsa, C. Magee, and G. Lux. An accurate and computationally efficient semi-empirical model for arsenic implants into single-crystal (100) silicon. Journal of Electronics Materials, 22(8):801-808, 1994.
[116] Z. Yu, D. Chen, L. So, and R.W. Dutton. PISCES-2ET and its applications subsystems. Integrated Circuits Laboratory. Stanford University. Stanford, California 94305, 1994.
[117] J.F. Ziegler. Ion Implantation: Science and Technology. Academic Press, San Diego, 1988.
[118] J.F. Ziegler, J.P. Biersack, and U. Littmark. The stopping and range of ions in solids. Pergamon Press, New York, 1985.